Aqueous solubility is an extremely important chemical property. It play a major role in defining the migration and ultimate fate of chemicals in the environment. For example:
CE 397: Environmental Risk Assessment Department of Civil Engineering, The University of Texas at Austin
4. Gas-Solid Interaction (nothing available)
5 Discussion of homework assignment #2
This lecture discussed the properties of chemical compounds. The
values of some of the descriptive coefficients described here can be found
in the NIST Chemistry Webbook.
The fate of a chemical in the environment depends, to a large extent, on the physical/chemical properties of that chemical, as well as the conditions/properties of the media within which the chemical exists.
There are many chemical properties that provide insight as to the preferred migration pathways and ultimate fate of chemicals on the environment. I have selected a small subset of those properties to discuss in lecture, based on their relative significance with respect to quantitative estimates of cross-media partitioning and mass transfer. It is important to recognize that these properties are not all-inclusive, i.e., there are many other chemical properties that lend insight regarding environmental fate, particularly as related to chemical transformations in the environment.
Solubility can be defined as the extent to which molecules of a pure compound (in its actual gaseous, liquid, or solid aggregation state) can be separated from other molecules of that compound and surrounded by molecules of a specific solvent. The solvent that we are most interested in is water. Aqueous solubility (S) can be defined as the abundance of chemical per unit volume of water when the solution is in equilibrium with the pure compoun at a specified temperature and pressure.

Aqueous solubility is an extremely important chemical property. It play
a major role in defining the migration and ultimate fate of chemicals in
the environment. For example:
Factors that Affect Solubility in Water:
![]()
where:
S = solubility in "fresh" water
S' = solubility in water containing salts
Ks = salting or "Setschenow" constant (L/mol)
[C]tm = total molar salt concentration (mol/L)
Over a wide range of chemicals, Ks varies from approximately 0.1 to 0.4 L/mol. For example, Schwarzenbach et al. report values ranging from 0.25 to 0.35 L/mol for several PAHs, and from 0.1 to 0.2 for simple benzene derivatives, e.g., 0.17 L/mol for toluene and 0.13 L/mol for phenol.
Magnitudes of Solubility
Chemical solubility ranges over many orders of magnitude in water (completely miscible to scarcely detectable). Some examples are provided below:
| Representative Chemical | Solubility (mg/l) | Temperature (Celcius) |
| Methanol | Total | 20 |
| methyl ethyl ketone (MEK) | 350,000 | 10 |
| MTBE | 48,000 | 25? |
| chloroform | 8,000 | 25 |
| Benzene | 1,800 | 25 |
| Trichloroethene (TCE) | 1,200 | 25 |
| Tetrachloroethene | 150 | 25 |
| Napthalene | 13 | 25 |
| Hexachlorobenzene | 0.006 | 25 |
Octanol-Water Partition Coefficient (Kow)
The octanol-water partition coefficient (Kow) is the ratio of a chemical's concentration in octanol to its concentration in the aqueous phase of a two-phase system at equilibrium.

![]()
The dimensionless octanol-water partition coefficient is one of the most important and frequently used properties to define chemical behavior in the environment. The use of 1-octanol was popularized by Hansch and Leo (1979) who focused on the use of this "property" to explain biochemical partitioning. However, it has since been used to study (and develop correlations) for partition coefficients between water and soil/sediment. It is also widely used to predict the distribution of chemicals in aqueous systems that contain an oily phase.
Octanol was originally selected because it has a carbon/oxygen ratio that is very similar to lipids. It is also readily available (and inexpensive) in its pure form, and is only sparingly soluble in water (approximately 600 mg/L).
Note that the range of chemical solubility in octanol tends to be fairly small (200 to 2,000 mol/m3). The variation in Kow between chemicals is dominated by variations in water solubility!
Kow varies over many orders of magnitude (10-3 > Kow > 107)
Typically use log10(Kow)
Magnitude of Kow
Some examples are provided below:
| Representative Chemical | Solubility (mg/l) | Log(Kow) |
| Methanol | Total | -0.77 |
| methyl ethyl ketone (MEK) | 350,000 | 0.26 |
| MTBE | 48,000 | 1.43 |
| chloroform | 8,000 | 1.97 |
| Benzene | 1,800 | 2.12 |
| Trichloroethene (TCE) | 1,200 | 2.47 |
| Tetrachloroethene | 150 | 2.97 |
| Napthalene | 13 | 3.17 |
| Hexachlorobenzene | 0.006 | 5.23 |
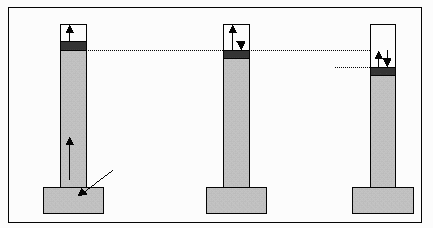
Vapor pressure (often referred to as equilibrium vapor pressure or pure-compound vapor pressure) can be defined as the pressure exerted by the vapor of a compound at equilibrium with its pure condensed phase, be it liquid or solid. Vapor pressure can be measured as shown in the diagram below. The grey material in each column is Mercury and in the leftmost column, a sample of the liquid whose vapor pressure is to be measured has been injected into the Mecury, rising to the top as its density is less than that of Mercury. The head space at the top of the Mecury column is initially a vacuum. As the liquid evaporates, its vapor pressure acts on the liquid surface, as shown in the central column, and depresses the level of the liquid surface as shown on the right column. The difference in level of the liquid surface, as measured in mm Hg, is the vapor pressure of the liquid.
A chemical's vapor pressure is important with respect to the rate at which it will volatilize or evaporate from the pure phase or from concentrated mixtures, e.g., gasoline. It is also useful in conjunction with other chemical properties, e.g., solubility in water, for estimating partition coefficients between air and water.
Vapor pressure is a strong function of:
Estimation based on Antoine's equation:
![]()
A, B, C = Antoine constants ---- tabulated for a wide range of chemicals
Errors: 2-6% for chemicals with Pvp > 10 mm Hg; 200-300% for low Pvp.
Excellent reference: Reid, Prausnitz, and Poling, "The Properties of Gases and Liquids, 4th ed., Appendix A, McGraw-Hill, New York, 1987).
The NIST Chemistry Webbook contains Antoine's equation coefficients for the vapor pressure of many chemical compounds
Vapor pressure is generally strongly correlated with boiling point (Tb)
For most VOCs, the following equation provides reasonable estimates of Pvp:
![]()
Where Pvp is in atm, T and Tb have units of K.
Magnitudes of Vapor Pressure
| Represenative Chemical | Solubility (mg/l) | log(Kow) | Pvp(mm Hg)@25 C | Tb(c) |
| MTBE | 48,000 | 1.43 | 249 | 55.2 |
| Chloroform | 8,000 | 1.97 | 198 | 61.7 |
| Methanol | total | -0.77 | 122 | 65 |
| MEK | 350,000 | 0.26 | 91 | 79.6 |
| Benzene | 1,800 | 2.12 | 95 | 80.1 |
| Trichloroethene (TCE) | 1,200 | 2.47 | 72 | 87.0 |
| Tetrachloroethene | 150 | 2.97 | 18 | 121 |
| Napthalene | 13 | 3.17 | 0.09 | 217.9 |
| Hexacholorobenzene | 0.006 | 5.23 | 0.000012 | 326 |
Molecular Diffusion Coefficients (Dl and Dg)
Recall:
![]()
D = molecular diffusion coefficient (L2/T)
Molecular diffusion coefficients are a function of:
Estimation Methods
Reasonably accurate methods have been developed for estimating diffusion coefficients in air and water, and account for the factors listed above. These methods have been presented in various sources, e.g., Handbook of Chemical Property Estimation Methods, Lyman et al., eds., American Chemical Society.
Several pages are attached to this handout and summarize some of the more common methods for estimating molecular diffusion coefficients in air and water. These pages are from a previous short course taught by Drs. H. Liljestrand and R. Corsi.
Magnitudes of Molecular Diffusion Coefficients (25 C)
| Representative Chemical | MW (g/mole) | Dair (cm2/s) | Dwater (cm2/s) |
| Methanol | 32.04 | 0.15 | 1.64E-5 |
| MEK | 72.11 | 0.081 | 9.8E-6 |
| Benzene | 78.1 | 0.087 | 1.1E-5 |
| MTBE | 88.15 | 0.079 | 9.4E-6 |
| Chloroform | 119.4 | 0.10 | 1.0E-5 |
| Napthalene | 128.17 | 0.059 | 7.5E-6 |
| Trichlorothene (TCE) | 131.4 | 0.079 | 9.1E-6 |
| Tetrachloroethene | 165.8 | 0.072 | 8.2E-6 |
| Hexachlorobenzene | 284.8 | 0.054 | 5.9E-6 |
The transfer of chemicals from liquid to gas, or vice-versa, is extremely important with respect to the migration of chemicals in the environment. In most (but not necessarily all) cases, the gaseous medium is air. However, the liquid medium may be water, a pure liquid phase of a chemical other than water, or a complex mixture of chemicals, e.g., gasoline or an oil spill.
For our purposes, we will discuss the interaction of chemicals between air and dilute aqueous solutions as well as between air and complex/concentrated mixtures of chemicals. We will begin with a discussion of equilibrium partitioning (Henrys law and Raoult's law), followed by a discussion of the kinetics of gas-liquid mass transfer.
Due to time constraints, much of the theory related to gas-liquid interaction will not be discussed. Where appropriate, you have been provided with hand-written notes, i.e., derivation of two-film theory, and references that allow for much greater insight regarding the underlying principles of gas-liquid mass transfer.
Examples of where gas-liquid interaction is important include:
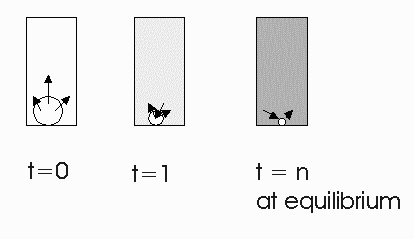
Henry's law applies to chemicals dissolved in dilute aqueous solutions that have reached equilibrium between the aqueous and adjacent air phase. At equilibrium for a fixed temperature and chemical the ratio of the chemical concentration in air to the chemical concentration in water is a constant referred to as the Henry's law constant.
At equilibrium:
![]()
The Henry's law constant is a valuable parameter that is required for estimating the equilibrium distribution of chemicals in unsaturated soil, rain droplets, etc. It is also important for estimating the rate of gas-liquid mass transfer for some chemicals (see below).
Units
It is conventional to define H in terms of gas concentrations in atmospheres and liquid concentrations in mol/m3.
Thus, the most typical units for H are atm-m3/mol
It is often easiest to work with "dimensionless" Henry's law constant (Hc) by converting gas concentrations from atmospheres to mol/m3. To do this we can invoke the ideal gas law:
![]()
Thus, it can be seen that:
![]()
R = the universal gas constant = 8.2 x 10-5 m3 gas-atm/mol-K
T = temperature (K)
Note that Hc really has units of mol/m3gas/mol/m3liq or m3liq/m3gas.
Henry's law constant is a strong function of:
Estimation Methods
It is commonly stated that Henry's law constant is simply the ratio of vapor pressure and solubility. This statement contains an important assumption that water is not very soluble in the chemical of interest because the vapor pressure that isused in the approximation is actually that of the pure chemical, whereas the solubility that is used is not of a pure chemical but that of the chemical saturated with water. An approximation of Henry's law constants based on vapor pressure and solubility breaks down when the solubility of water in the chemical actually exceeds a few percent
However, the use of vapor pressure and solubility can lead to good estimates of H for many chemicals of interest to environmental risk (exposure) assessment. When using these properties it is important to recognize the temperatures at which the vapor pressure and solubility were measured or estimated (particularly for the vapor pressure).
Several researchers have studied the influence of temperature on Henry's law constants. Correlations have been developed between water temperature and H for many chemicals.
These equations generally take the form of
![]()
Gossett, J.M., "Measurement of Henry's Law Constants for C1 and C2 Chlorinated Hydrocarbons," ES&T, 21(2): 202-208 (1987).
Ashworth , R.A., et al., "Air-Water Partitioning Coefficients of Organics in Dilute Aqueous Solutions," Journal of Hazardous Materials, 18: 25-36 (1988).
Henry's Law Constants on the Web
This equation is of a form similar to Antoine's equation (with C = 0), suggestion that Henry's law constants vary with temperature in a manner similar to vapor pressure. In fact, if A and B values can not be found, it is common to estimate the ratio of H values at two temperatures as the ratio of Pvp at those same two temperatures.
Magnitudes of Henry's law constants (25 C)
| Representative Chemical | Solubility (mg/l) | Pvp (mm Hg) | H (atm-m3/mol) | A | B |
| MTBE | 48,000 | 249 | 5.9E-4 | ||
| Chloroform | 8,000 | 198 | 3.7E-3 | 9.843 | 4612 |
| Methanol | total | 122 | 6.9E-6 | ||
| MEK | 350,000 | 91 | 1.3E-4 | -26.32 | -5214 |
| Benzene | 1,800 | 95 | 5.3E-3 | 5.534 | 3194 |
| Trochloroethene | 1,200 | 72 | 9.6E-3 | 11.37 | 4780 |
| Tetrachloroethene | 150 | 18 | 1.8E-2 | 12.45 | 4918 |
| Napthalene | 13 | 0.09 | 4.8E-4 | ||
| Hexachlorobenzene | 0.006 | 0.000012 | 5.4E-4 |
A and B values lead to H in atm-m3/mol
Henry's law applies to dilute aqueous solutions. It should not be applied to predict equilibrium partition coefficients between other liquid solutions and air, e.g., gasoline or oil. Instead, a number of other approximations have been developed to estimate liquid-air partition coefficients for non-aqueous solutions. One of these, Raoult's law (actually the Raoult-Dalton equilibrium law) is often used for ideal solutions and generally yields good approximations of liquid-air partitioning for most applications of interest in environmental risk assessment
The Raoult-Dalton equilibrium law is shown below:
Raoult's law:
![]()
pA = equilibrium partial pressure of chemical A in vapor adjacent to liquid
xA = mole fraction of A in liquid phase
Dalton's law:
![]()
![]()
yA = mole fraction of A in vapor phase
P = total pressure of system
Raoult-Dalton Equilibrium Law
![]()
Henry's law and the Raoult-Dalton law both apply only to systems at equilibrium. However, some systems may take a very long time to reach an equilibrium condition, while others may never even reach equilibrium, e.g., chemical volatilization from a hazardous waste pond to the ambient atmosphere. Thus, it is important to be able to estimate the net rate of mass transfer across a gas-liquid interface. This rate depends on how close a system is to equilibrium, i.e., the rate is fastest when a system is far from equilibrium and approaches zero as a system approaches equilbrium.
Dilute Aqueous Systems
For dilute aqueous systems the following expression can be derived for the rate of mass transfer across an interface:
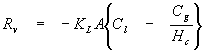
where
Rv = rate of mass transfer from water to adjacent air (M/T)
KL = overall mass transfer coefficient (L/T)
A = surface area between water and air (L2)
Cl = chemical concentration in water (M/L3)
Cg = chemical concentration in adjacent air (M/L3)
Note that this equation can be derived from any of a number of mass transfer theories (two-film theory, penetration theory, film-penetration theory). I have attached a hand-written derivation based on two-film theory.
Overall Mass Transfer Coefficient:
Mass transfer across the interface increases with an increase in the overall mass transfer coefficient. Therefore, the inverse of KL can be thought of as an overall resistance to mass transfer.
Based on two-film theory, the overall mass transfer resistance can be conceptualized as the sum of resistance on the liquid and gas sides of the air-water interface:
![]()
where
kl = liquid-phase mass transfer coefficient (L/T)
kg = gas-phase mass transfer coefficient (L/T)
Note that the first term on the right-hand-side of the above equation corresponds to a liquid-phase resistance to mass transfer while the second terms corresponds to gas-phase resistance to mass transfer.
For most environmental systems, the ratio of kg to kl is greater than 10. Thus, for chemicals with Henry's law constants that are much lower than 0.1, gas-phase resistance to mass transfer can dominate the overall mass transfer process. Conversely, for chemicals with large values of Hc, mass transfer is typically dominated by the liquid phase and the second term on the right-hand side can be neglected.
Theoretical formulations of kl and kg
The primary difference between mass transfer theories is in the theoretical formulation of liquid and gas-phase mass transfer coefficients.
For two-film theory:
![]()
![]()
Where dl and dg correspond to liquid and gas-phase film thickness, respectively.
For penetration theory:
![]()
![]()
where rl and rg are liquid and gas-phase surface renewal rates.
Note that while film thickness and surface renewal rates can not be measured and do not allow us to determine liquid and gas-phase mass transfer coefficients from first principles, they do allow some insight into the overall mass transfer process. For example, each of these variables should conceptually be a strong function of the amount of kinetic energy on either the liquid or gas side of the interface. Thus, liquid and gas-phase mass transfer coefficients are a function of both the flow properties and chemical properties, the latter of which are also affected by fluid conditions.
Relating mass transfer coefficients between chemicals:
The ratio of liquid-phase (or gas-phase) mass transfer coefficients between two chemicals can be determined using the equations listed above:
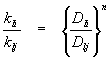
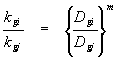
Where n and m vary between 0.5 and 1.0 in accordance with penetration and two-film theories. Values of the exponents tend toward 0.5 as the amount of turbulent kinetic energy in a system increases. A value of 2/3 is often used as a "punt".
The significance of these equations can not be overlooked. They allow estimates of liquid and gas-phase mass transfer coefficients for a chemical if such values are known for another chemical, as long as the molecular diffusion coefficients for the two chemicals are known.
For specific environmental systems, liquid-phase mass transfer coefficients can be determined using highly-volatile tracer chemicals. Gas-phase mass transfer coefficients can be determined using lower-volatility (low Hc) chemicals. For many systems, empirical correlations have been developed to estimate liquid-phase mass transfer coefficients. Gas-phase mass transfer coefficients are generally more difficult to estimate, and are often estimated based on assumed ratios of kg/kl.
Non-Aqueous Phases
The discussion provided above is valid only for those systems involving water and air. Mass transfer across the interface of a non-aqueous solution is generally more difficult to estimate. The following equation generally used:
![]()
Here, Cgi corresponds to the concentration of a chemical in the gas-phase immediately adjacent to the non-aqueous liquid surface. It is often estimated based on the Raoult-Dalton equilibrium law.
Note that liquid-phase resistance to mass transfer has been neglected in this analysis. In general, gas-phase mass transfer coefficients that are used for aqueous applications can be used here. However, the same is not true for liquid-phase mass transfer coefficients. There is a paucity of information in the published literature related to liquid-phase mass transfer coefficients for non-aqueous phases. Thus, it is often assumed that the non-aqueous liquid phase has a uniform concentration throughout, including the immediately liquid-side of the interface, i.e., a liquid-film thickness is neglected.
The adsorption of chemicals to solid surfaces often plays an important role in the ultimate fate and impact of chemicals in/on the environment. For example, chemicals with low solubility and low vapor pressure, or conversely those with large octanol-water partition coefficients, may preferentially sorb to sediment in lakes. As the sediment settles to the bottom of the like, bottom sediment can serve as a "reservoir" within which such chemicals accumulate. Chemicals that adsorb to soil particles are, at least temporarily, immobilized and will not travel through a soil column as rapidly as infiltrating water. However, such sorption leads to longer retention times in the soil column, with the potential for slow desorption years after the chemicals were originally discharged to the soil. In indoor environments, adsorption to solid surfaces (e.g., carpeting, gypsum board, upholstery) can be quite significant, leading to short-term reductions in indoor air concentrations but longer chemical retention times within a building.
The state of understanding regarding the rate of chemical adsorption and desorption from solids is poor. However, several researchers have studied the extent of chemical partitioning between solids and water at equilibrium. For most applications, the concentrations of chemicals in the environment are low enough that linear adsorption isotherms are valid. Thus, the equilibrium relationship between solids and water is typically expressed as:
![]() where
where
Cs = concentration of chemical on solids (mg/kg)
Cl = concentration of chemical in water (mg/L)
Kp = solid/water partition coefficient (L/kg)
In the 1970s and early 1980s, studies by agricultural chemists lead to the conclusion that hydrophobic organic chemicals tend to sorb to organic carbon present in soils. These observations were also made for bottom sediments in lakes.
Several expressions have since been developed to relate solid/water partition coefficients (Kp) to organic carbon partition coefficients (Koc).
![]()
Where
Koc = organic carbon partition coefficient (L/kg)
foc = fraction of solid made up of organic carbon (g-carbon/g-solid)
Several empirical relationships have been developed to relate Koc to the octanol/water partition coefficient of hydrophobic chemicals. Several relationships are provided below:
![]()
The units of Koc for this expression are L/g-solids. This equation was developed for chemical sorption to the organic phase of solids existing in various types of wastewaters.
![]()
![]()
The units of Koc for the last two expressions are L/kg. Each expression was developed to predict chemical sorption to sediment, but are often applied to soil.
Return to the Class Home Page
![]()