CE 397: Environmental Risk Assessment
Department of Civil Engineering
The University of Texas at Austin
Lecture Notes: Class #3 -
Transport Processes, Richard Corsi, Jan 27, 1998Readings:
Introduction
The importance of transport processes in environmental risk assessment is the prediction of transport or migration of chemicals in the environment.
The fundamental mechanisms are advection, diffusion and dispersion (turbulent diffusion).
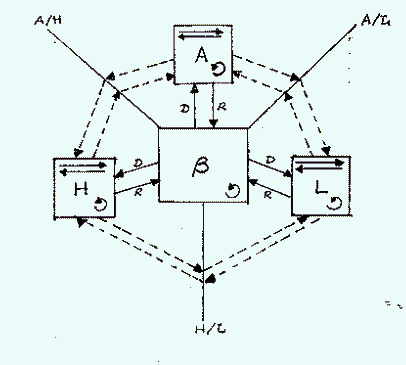
The environment may be viewed as connected spheres:

Where:
B = biosphere
L = lithosphere
H = hydrosphere
A = atmosphere
D = discharge
R = recharge
The double arrows in each "sphere" box indicate transport within a sphere. The "A/L" designation indicates an interface between the atmosphere and the lithosphere across which there may be transfer. The circular arrow in each "sphere" represents the physical, chemical or biological reactions that take place in each sphere. These reactions can change the concentrations of a chemical or transform a chemical into another chemical species. In environmental risk assessment we are concerned with what ends-up in the biosphere.
Advection
Advection is defined as movement of a chemical by virtue of its presence in a medium which happens to be flowing, (Mackay, 1991).
Rate of Advection = NA = Q*C (mass/time)
Q = flow rate of advecting medium (m3/hr)
C = concentration of chemical in medium (mg/m3)
Important advection processes in air and water systems:
Diffusion
Diffusion is a redistribution of chemical mass within a phase induced by Brownian motion and tending toward uniformity. Brownian motion is thermal energy due to random molecular collisions. There is motion in all directions, but there is a tendency for the chemical to move from areas of high concentration to areas of low concentration.
Rate of molecular diffusion (ND):

Typically diffusion coefficients are on the order of 10-5 m2/sec in air and 10-9 m2/sec in water. Diffusion coefficients are a function of chemical properties. Generally, larger molecules have smaller diffusion coefficients. Diffusion coefficients are also a function of temperature. At higher temperatures the diffusion coefficients are larger.

As an example, diffusion through 1 m of water with D = 2x10-9 m2/sec = 2.5x108 sec ~ 8 years.
Dispersion (Turbulent Diffusion)
Turbulent motions are deviations from the mean flow.
There is thermally generated turbulence - for example air layers that are warmer near the earth's surface have acceleration upwards that generate the turbulence in the atmosphere. There is mechanically generated turbulence caused by a fluid flowing over a stationary surface, which can induce perturbations in the flow.
The mechanisms that tend to suppress dispersion include temperature or density differences and viscosity.
Advection-Diffusion Equation
In differential form is a mass balance over a differential control volume in the flow field.
The mass balance in words is:
Accumulation = Inflow - Outflow +/- Reactions
The final form of the equation, when there are no reactions and the control volume is constant, is:
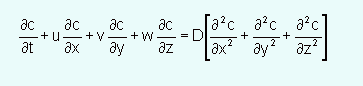
This is an instantaneous expression, the turbulence is in the flow field, so the turbulence is "hidden" in the velocity terms.
Turbulent Transport
Atmospheric turbulence can be evaluated by looking at the variations in the wind speed in a single direction.
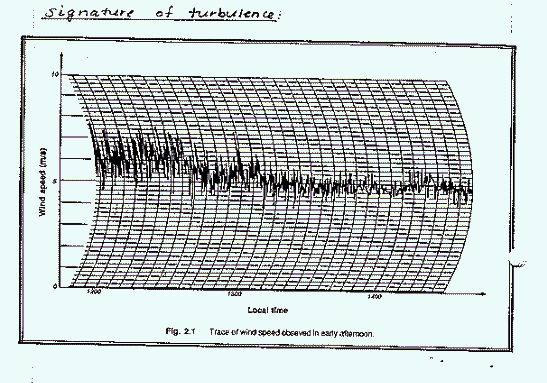
Where there is greater variation in the wind speed (at early times on the above figure) there is higher intensity turbulence. The instantaneous velocity for example, u, can be decomposed into an area weighted average velocity and a variation term, u':
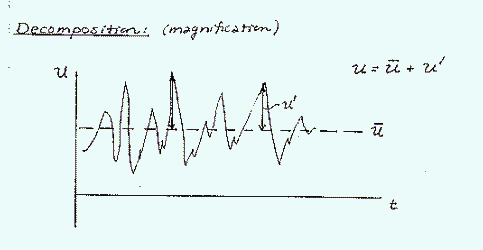
Substituting the decomposed velocity terms into the advection-diffusion equation and rearranging terms, yields an equation with a new group of averaged fluctuation partial differential terms. These new terms are the dispersion, which represent the turbulent transport of mass:
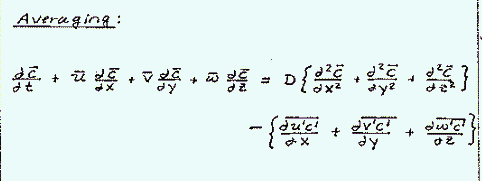
These turbulent transport terms are very important in atmospheric systems and rivers.
The values to use in a particular situation for these terms are not easy to determine. Typically a first-order gradient approximation is used. The approximation is an analogy to molecular diffusion.
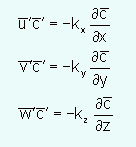
The k terms are eddy diffusion coefficients and in the atmosphere have values near 1-5 m2/sec. Using these terms the advection-diffusion equation that is used for most atmospheric transport models is:
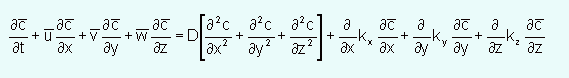
Reactor Analysis Approach
A control volume of the environment is modeled as a continuous flow stirred tank reactor (CFSTR):
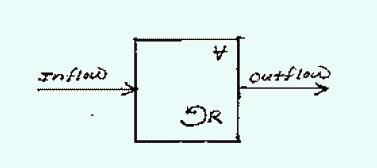
Some examples of control volumes of interest are:
The mass balance for the reactor in words is:
Rate of mass accumulation = rate of mass inflow - rate of mass outflow +/- rate of mass removal (or generation)
Because of the CFSTR assumptions the concentration is uniform within the control volume and is equal to the concentration leaving the control volume. Each control volume is therefore a homogeneous segment of the system. In this way the reactor approach is an approximation for the actual system. For a particular system multiple reactors in series, or combined in series and parallel, can be used to model the environment.

The layered system could be used to model an estuary, layers in an airshed or a sewer pipe. The axial dispersion is minimized with an increasing number of reactors.
Return to the Class Home Page