CE 397: Environmental Risk Assessment
Department of Civil Engineering , The University of Texas at Austin
Solution to Assignment #1: Statistical Analysis of Environmental Data
Difference in Means Between two Data Sets
(a) Statistics of the Original 90 Benzene Values (in mg Benzene / kg soil) :
|
Column1 |
|
| Mean |
258704 |
| Standard Error |
166934 |
| Median |
500 |
| Mode |
19 |
| Standard Deviation |
1583676 |
| Sample Variance |
2508030041719 |
| Kurtosis |
78 |
| Skewness |
8.62 |
| Range |
14599999 |
| Minimum |
1 |
| Maximum |
14600000 |
| Sum |
23283324 |
| Count |
90 |
The range of the data is 1 mg/kg to 14,600,000 mg/kg or 14.6 gm Benzene / kg soil. The mean is 258,700 mg/kg, the median is 500 mg/kg. Since the mean is much greater than the median, these data contain a small number of very large values that strongly influence the value of the mean and make it not a very good indicator of the midrange of the data. The Coefficient of Skewness = 8.62 which shows that the data are highly positively skewed.
(b) Statistics of the logarithms to base 10 of the 90 benzene data:
|
Log C |
|
| Mean |
2.837 |
| Standard Error |
0.167 |
| Median |
2.699 |
| Mode |
1.279 |
| Standard Deviation |
1.588 |
| Sample Variance |
2.521 |
| Kurtosis |
-0.121 |
| Skewness |
0.534 |
| Range |
7.289 |
| Minimum |
-0.125 |
| Maximum |
7.164 |
| Sum |
255.363 |
| Count |
90 |
| Confidence Level(95.0%) |
0.333 |
The coefficient of skewness of these data is 0.534, which is much more reasonable. The median is 2.699 and the mean is 2.837. These values correspond to in the real space to 102.699 = 425 mg/kg and 102.837 = 687 mg/kg, respectively, which are reasonable values for the midrange of the data. The fact that the mean is greater than the median is consistent with the fact that the data are positively skewed
The logarithms are a better representation of the data than the original values because the range has been greatly reduced (now –0.125 to 7.164) and the data are distributed in a more reasonable way over that range.
The histogram of the logarithms of the data:
|
-2 |
Frequency |
Cumulative % |
|
-1 |
0 |
.00% |
|
0 |
2 |
2.22% |
|
1 |
9 |
12.22% |
|
2 |
21 |
35.56% |
|
3 |
20 |
57.78% |
|
4 |
20 |
80.00% |
|
5 |
7 |
87.78% |
|
6 |
7 |
95.56% |
|
7 |
3 |
98.89% |
|
8 |
1 |
100.00% |
|
9 |
0 |
100.00% |
| More |
0 |
100.00% |
The exceedence probability is estimated as P(C>c*) = m/(n+1), where m is number of data values fulfilling that condition, and n is the total number of data values (n = 90).
| Threshold Concentration, c* | Number of samples exceeding c* | Exceedence Probability |
| 1000 | 38 | 38/91 = 0.418 |
| 10000 | 18 | 18/91 = 0.198 |
| 100000 | 11 | 11/91 = 0.121 |
Note that there are two values of exactly 1000 mg/kg and these have not been considered in the calculation of the exceedance probability since we are seeking the exceedence probability and these values equal but do not exceed the threshold concentration. A similar conclusion holds for the single value of 100 mg/kg. The exceedance probabilities of the last 30 values and the last 60 values in the data set are shown below. In general, the last values of the data set have a lower chance of exceeding threshold levels than does the data set as a whole.
| Threshold Concentration, c* | Exceedance Prob with 30 data | Exceedence Prob with 60 data |
| 1000 | 11/31 = 0.355 | 30/61 = 0.492 |
| 10000 | 6/31 = 0.194 | 17/61 = 0.279 |
| 100000 | 2/31 = 0.065 | 4/61 = 0.066 |
4. Recursive Estimation of the Mean
The logs of the data have been analyzed to estimate the standard error of the mean and thus the approximate 95% confidence limits on the mean with the result appearing as:
| N | Values | Log(C) | Mean | Stdev | Stdev/n^0.5 | m+2Se | m-2Se |
|
1 |
2180 |
3.338 |
3.338 |
||||
|
2 |
90 |
1.954 |
2.646 |
0.979 |
0.692 |
4.031 |
1.262 |
|
3 |
477 |
2.679 |
2.657 |
0.692 |
0.400 |
3.457 |
1.858 |
|
4 |
4400 |
3.643 |
2.904 |
0.750 |
0.375 |
3.654 |
2.153 |
|
5 |
18 |
1.255 |
2.574 |
0.983 |
0.439 |
3.453 |
1.695 |
|
6 |
70 |
1.845 |
2.453 |
0.928 |
0.379 |
3.210 |
1.695 |
|
7 |
310 |
2.491 |
2.458 |
0.847 |
0.320 |
3.098 |
1.818 |
|
8 |
490 |
2.690 |
2.487 |
0.789 |
0.279 |
3.045 |
1.929 |
|
9 |
300 |
2.477 |
2.486 |
0.738 |
0.246 |
2.978 |
1.994 |
|
10 |
350 |
2.544 |
2.492 |
0.696 |
0.220 |
2.932 |
2.052 |
|
11 |
6000 |
3.778 |
2.609 |
0.766 |
0.231 |
3.070 |
2.147 |
|
12 |
1500 |
3.176 |
2.656 |
0.748 |
0.216 |
3.088 |
2.224 |
|
13 |
82 |
1.914 |
2.599 |
0.745 |
0.207 |
3.012 |
2.186 |
|
14 |
210 |
2.322 |
2.579 |
0.720 |
0.192 |
2.964 |
2.194 |
|
15 |
460 |
2.663 |
2.585 |
0.694 |
0.179 |
2.943 |
2.226 |
|
16 |
1800 |
3.255 |
2.627 |
0.691 |
0.173 |
2.972 |
2.281 |
|
17 |
120 |
2.079 |
2.594 |
0.682 |
0.165 |
2.925 |
2.264 |
|
18 |
86 |
1.934 |
2.558 |
0.680 |
0.160 |
2.878 |
2.237 |
|
19 |
510 |
2.708 |
2.566 |
0.662 |
0.152 |
2.869 |
2.262 |
|
20 |
130 |
2.114 |
2.543 |
0.652 |
0.146 |
2.835 |
2.252 |
|
21 |
1600 |
3.204 |
2.575 |
0.651 |
0.142 |
2.859 |
2.290 |
|
22 |
360000 |
5.556 |
2.710 |
0.899 |
0.192 |
3.093 |
2.327 |
|
23 |
750 |
2.875 |
2.717 |
0.879 |
0.183 |
3.084 |
2.351 |
|
24 |
30 |
1.477 |
2.666 |
0.896 |
0.183 |
3.031 |
2.300 |
|
25 |
270 |
2.431 |
2.656 |
0.879 |
0.176 |
3.008 |
2.305 |
|
26 |
8 |
0.903 |
2.589 |
0.927 |
0.182 |
2.952 |
2.225 |
|
27 |
109 |
2.037 |
2.568 |
0.915 |
0.176 |
2.921 |
2.216 |
|
28 |
44 |
1.643 |
2.535 |
0.915 |
0.173 |
2.881 |
2.190 |
|
29 |
86 |
1.934 |
2.515 |
0.905 |
0.168 |
2.851 |
2.178 |
|
30 |
1100 |
3.041 |
2.532 |
0.895 |
0.163 |
2.859 |
2.205 |
Or in graphical form as:
It can be seen that there is little reduction the error
of estimate of the mean after about 15 samples because a longer sample
brings in additional areas of the site that have differing concentration
levels. Thus the statistical sample is not homogeneous, so adding more
data from further afield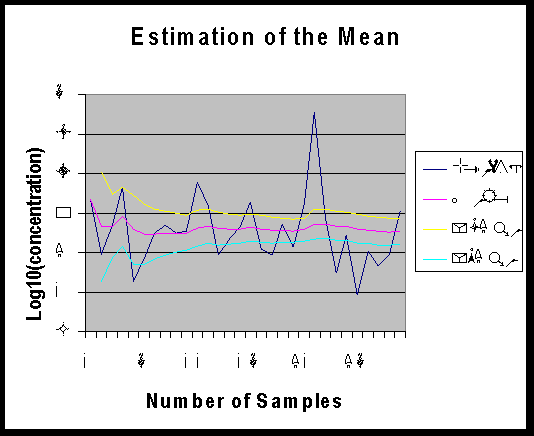 
increases
the variance of the data set which offsets the reduction in the standard
error of the mean with the square root of the number of samples.
5. T-test for the Difference in Two Means
For the original data, the means and standard deviations of the first and second 45 data values are:
| First 45 | Second 45 | |
| Mean |
13957 |
503451 |
| StDev |
57593 |
2224234 |
| Coeff var |
4.12 |
4.42 |
It can be seen that the standard deviation is much greater than the mean in both cases, so it doesn’t make a lot of sense to use the normal distribution to study these data since there is a high chance of getting a negative concentration and that isn’t physically reasonable. The coefficient of variation is the ratio of the standard deviation to the mean, which is about 4 in both data sets, so their relative variability is about the same, but the mean value is higher in the second set than in the first.
Lets use the logs of the data for the test instead, since these data are more nearly normally distributed.
| First 45 | Second 45 |
|
2.513 |
3.162 |
|
1.105 |
1.914 |
If X = the logs to base 10 of the first 45 data and Y = the logs to base 10 of the second 45 data, then the t statistic is computed as:
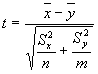
with m = n = 45, this result is found to be:
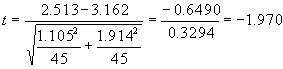
What this calculation says is that the difference between the two means of –0.649 is about twice the standard deviation of the pooled sample, 0.329. This is on the borderline of being considered a statistically significant difference. In general, if the t statistic is > 2 or < -2 then the difference in the means is statistically significant, and if |t| < 2, the hypothesis that there is no difference between the two means cannot be rejected.
To be more precise, we should find the t statistic value for n = n+m-2 = 88 degrees of freedom = 88, for which the values are (from Probability Concepts in Engineering Planning and Design, Vol. 1, Table A.2, by A. H-S. Ang and W.H. Tang, Wiley Publishers, 1975):
| Percentile Value | 0.9 | 0.95 | 0.975 | 0.99 |
| T statistic | 1.29 | 1.65 | 1.98 | 2.36 |
This means that the observed t-statistic is about at the 95% confidence limit since that limit has a range on the percentile value from (0.025 to 0.975).
Return to the Class Home Page