Homework 1 Solution
GIS in Water Resources
Fall 2010
Prepared by David R. Maidment
1.
Map Projection Parameters
The map below shows Utah and the display
parameters of the State Plane coordinate system for the Utah Central Zone.
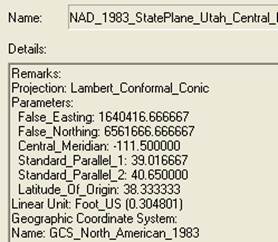

(a) Sketch on the map the standard parallels, the
central meridian and the latitude of origin of this projection.
I prepared the map above using ArcGIS Explorer Online. http://explorer.arcgis.com/ The tool for
locating coordinates is called Measure ![]() and when you click on that tool, it invokes a
dialog box
and when you click on that tool, it invokes a
dialog box  within which the
within which the ![]() icon serves to select identifying a point
location. Utah is clearly defined in
latitude-longitude coordinates using meridians at 109°W and 114°W and parallels
at 37°N and 42°N, making it 5° longitude x 5° latitude in area, except for a
box 2° longitude x 1° latitude that is omitted in the upper right corner (I
imagine the reason for this would make an interesting historical study!)
icon serves to select identifying a point
location. Utah is clearly defined in
latitude-longitude coordinates using meridians at 109°W and 114°W and parallels
at 37°N and 42°N, making it 5° longitude x 5° latitude in area, except for a
box 2° longitude x 1° latitude that is omitted in the upper right corner (I
imagine the reason for this would make an interesting historical study!)
(b) For this projection, what are the coordinates
of the origin (fo, lo) and the corresponding (Xo, Yo) ?
(fo,
lo)
= (38° 20’ N, 111° 30’ W)
(Xo, Yo) = (1640416.666667, 6561666.666667) in meters.
Notice that the (fo, lo) are stated with the vertical coordinate first and the horizontal coordinate second, while the reverse is true for (Xo, Yo)
(c) What earth datum is used in this coordinate
system?
The earth datum is GCS (Geographic Coordinate System) North American of 1983, or NAD83.
(d) What map projection is used in this
coordinate system?
Lambert Conformal
Conic
2. Locations on the Earth
Using ArcGIS Explorer and putting in the names of Austin, Logan and Lincoln reveals the following designated locations for these cities. Convert these locations into decimal degrees.
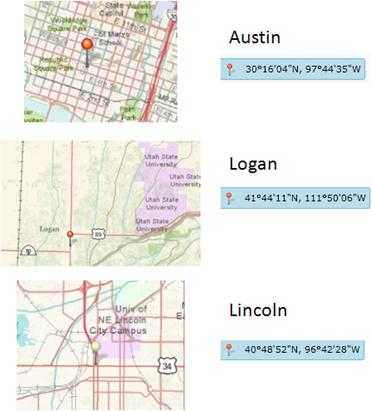
The computations are shown in the spreadsheet below.
LatDD = LatDeg + LatMin/60 + LatSec/3600
LongDD = -(LongDeg + LongMin/60 + LongSec/3600)
So, for Austin,
LatDD = 30 + 16/60 + 4/3600 = 30.2678
LongDD = -(97+44/60 + 35/3600) = -97.7431
|
LatDeg |
LatMin |
LatSec |
LongDeg |
LongMin |
LongSec |
LatDD |
LongDD |
|
|
Austin |
30 |
16 |
4 |
97 |
44 |
35 |
30.2678 |
-97.7431 |
|
Logan |
41 |
44 |
11 |
111 |
50 |
6 |
41.7364 |
-111.8350 |
|
Lincoln |
40 |
48 |
52 |
96 |
42 |
28 |
40.8144 |
-96.7078 |
The smallest unit that distinguishes location in degrees, minutes and seconds is 1 arc second. This corresponds to 1/3600 = 0.000278 decimal degrees. It follows that locations in decimal degrees must be specified to at least 4 decimal places if location precision is not to be lost when conversions into decimal degrees are done. Also, please note that in the western hemisphere, decimal longitudes are always negative. In other word decimal degrees are positive or negative numbers not numbers with W or N associated with them.
3. Great Circle Distances
![]() The great circle distance is given
by the formula
The great circle distance is given
by the formula
with R = 6378.137 km.
All the angles need to be in radians for formulas in Excel to work, so the above angles are converted as shown below:
|
|
LatDD |
LongDD |
LatRad |
LongRad |
||
|
Austin |
30.2678 |
-97.7431 |
0.528272 |
-1.70594 |
||
|
Logan |
41.7364 |
-111.8350 |
0.728437 |
-1.95189 |
||
|
Lincoln |
40.8144 |
-96.7078 |
0.712346 |
-1.68787 |
||
|
|
||||||
And the corresponding great earth distances are computed as follows:
|
R = |
6378.137 |
|||
|
Austin-Logan |
LatRad, f |
LongRad, l |
Distance km |
|
|
A |
0.5283 |
-1.7059 |
1795.473 |
|
|
B |
0.7284 |
-1.9519 |
||
|
Austin-Lincoln |
LatRad, f |
LongRad, l |
Distance km |
|
|
A |
0.5283 |
-1.7059 |
1177.762 |
|
|
B |
0.7123 |
-1.6879 |
||
|
Logan-Lincoln |
LatRad, f |
LongRad, l |
Distance km |
|
|
A |
0.7284 |
-1.9519 |
1268.081 |
|
|
B |
0.7123 |
-1.6879 |
||
In order to check the distances between the two points, I used ArcGIS Explorer at http://explorer.arcgis.com . I marked the three cities as described above, and then I used a measure tool to measure between pairs of marked locations. Here is an example for the distance between Logan and Lincoln, for which I got 1267.787 km, as compared to 1268.081 km above (a difference of 0.294 km, or 294 m), which seems reasonable given that the great circle distance we’ve computed is on a spherical earth.

The distance between Austin and Logan is 1795.183 km, and between Austin and Lincoln is 1178.257 km which are both very close to the answers given above. Actually, it’s a bit hard to zoom into these points exactly in ArcGIS Explorer when doing this “measure” so if you could do that better, the results would probably be closer to those computed by the great circle formula.
4. Size of DEM cells
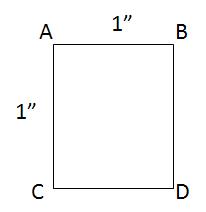
The distances AB and AC, and be computed by the formulas for
distance along a parallel and a meridian, with Re = 1378.137 km.
![]()
![]()
There is a very slight difference in the latitude f between the top and bottom of a DEM cell, but let’s neglect that for this example, so , the area of the DEM cell is given by
![]()
The results of a spreadsheet computation of these formulas are shown below:
|
DEM Cells |
R = |
6378.137 |
Df, Dl = |
4.848E-06 |
|
LatRad, f |
LongRad, l |
Cosf |
AB |
AC |
Area |
Sqrt(Area) |
|
|
Austin |
0.5283 |
-1.7059 |
0.8637 |
26.707 |
30.922 |
825.828 |
28.737 |
|
Logan |
0.7284 |
-1.9519 |
0.7462 |
23.075 |
30.922 |
713.513 |
26.712 |
|
Lincoln |
0.7123 |
-1.6879 |
0.7568 |
23.403 |
30.922 |
723.662 |
26.901 |
The great circle formula given above is erroneous when applied to very short distances. In that case, an alternative great circle formula called the “Haversine formula” can be used, as follows:
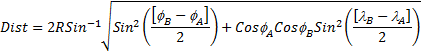
In this case, for the distance along a parallel ![]() can
be given by the latitude of the location.
Doing the calculations this way gives the following results, which are
identical to the ones given above for the simple formulas for distance along a
meridian and parallel.
can
be given by the latitude of the location.
Doing the calculations this way gives the following results, which are
identical to the ones given above for the simple formulas for distance along a
meridian and parallel.
|
DEM Cells |
R = |
6378.137 |
Df, Dl = |
4.848E-06 |
|||
|
LatRad, f |
LongRad, l |
Cosf |
AB |
AC |
Area |
Sqrt(Area) |
|
|
Austin |
0.528272 |
-1.7059381 |
0.8636792 |
26.707 |
30.922 |
825.828 |
28.737 |
|
Logan |
0.728437 |
-1.951889 |
0.7462155 |
23.075 |
30.922 |
713.513 |
26.712 |
|
Lincoln |
0.712346 |
-1.6878691 |
0.7568303 |
23.403 |
30.922 |
723.662 |
26.901 |
The fact that these two results are identical can also be demonstrated mathematically.
For distance along a
parallel, ![]() and in this case the Haversine
formula reduces to
and in this case the Haversine
formula reduces to

![]()
![]()
as was given earlier in the simple formula for distance along a parallel.
For distance along a
meridian, ![]() so the Haversine
formula reduces to:
so the Haversine
formula reduces to:

![]()
![]()
as was given earlier in the simple formula for distance along a meridian.