TERM PROJECT
CE394K SURFACE WATER HYDROLOGY
UNIVERSITY OF TEXAS AT AUSTIN
A GIS ASSESSMENT OF NONPOINT SOURCE POLLUTION
LOAD IN AUSTIN
By Christine Dartiguenave
Graduate Research Assistant
Center for Research in Water Resources
J.J Pickle Research Campus Bldg.119
Austin, TX 78712
Email : darti@mail.utexas.edu
December 1996
Table of contents
- Introduction
- Presentation of the map-based model
- Principle
- Why using 30 m DEM's?
- Build the flow direction grid
- Digital elevation model processing
- Burn in process and flow direction computation
- Delineate the watersheds
- From the stream links
- From the stations coverages
- Get the coordinates of the gage stations
- Create the necessary text files
- Generate the point coverages
- Adjust the coverages
- Delineate the watersheds
- Comparison
- Build a rainfall runoff grid
- Discharge
- Precipitation
- Rainfall runoff relationship
- Build an EMC grid
- Build a grid giving the pollutant load associated to each cell
- NPS pollution loading assessment
- Conclusion
As a graduate assistant, I am involved in a map-based modeling project
sponsored by the City of Austin. The goal of this research project is to build a model which can evaluate annual nonpoint source pollution loading in Austin creeks in function of different scenarios of land use:
- current conditions
- future conditions
- future conditions with City mandated BMPs
- simulation one year construction period for all vacant land areas
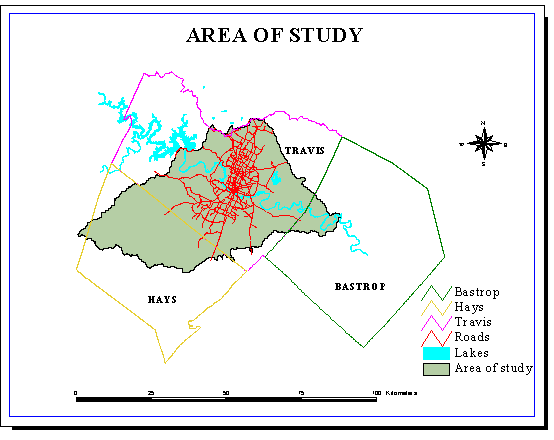
The area of study does not correspond to a particular juridiction (county...) but to a hydrologic entity (drainage area).
The model will allow to evaluate the actual effectiveness of Best
Management Practices (BMP's) for the control of nonpoint source pollution.
It will also enable to determine the contribution of any jurisdiction (City, county...) to the pollution load, and then be a first tool towards decision-making processes for remediation decisions.
The annual pollution load is the product of the discharge by the concentration:
Load (mass/year) = Q(volume/year) * C(mass/volume)
The model uses a digital discretization, or grid representation, of a watershed for the approximation of average annual pollutant loading.
The procedure is the following:
- Build a flow direction grid using the DEM's.
- Delineate the watersheds.
- Build a grid with rainfall runoff values.
- Build a grid with Estimated Mean Concentration (EMC) values.
- Multiply the two last grids together to get a grid whose each cell has the annual loading value it is responsible for.
- Build a weighted-flow accumulation grid from the flow direction grid (weighted with the annual loading values).
The annual loading in any cell corresponds to the value of this cell in the weighted flow accumulation grid.
Digital Elevation Models (DEM's), which consist of a sampled array of elevations for ground positions at regularly spaced intervals, are used to build the flow direction grid and hence to delineate the watersheds.
A study has already be made for Austin with 90 m DEM's (Francisco Olivera, Spatial Hydrologic Databases of Austin).
But some of the delineations are really not good at all.
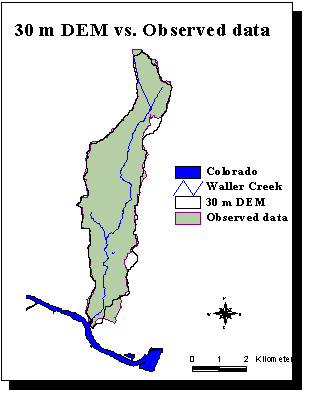
There is a 44% relative error between the areas observed on the field and delineated with the 90 m DEM's for Waller Creek, which is a small urban watershed (cf. following map).
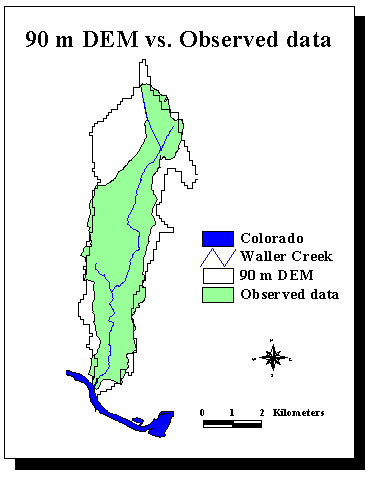
Or it is very important to define as accurately as possible the drainage area corresponding to the gage stations as their data are used to build the model.
There was a need to improve the delineations realized with 90 m DEM's. 30 m DEM's (i.e. one elevation value for every 30m/30m square) are now available for the area of study. They give about 10 times more information than 90 m DEM's. The 30 m DEM's used are each composed of about 190,000 cells. Until now,
I have received from the City 9 DEM's, which cover the east part of Austin, from the City. They correspond to about 1,700,000 cells. The following map shows in green the watersheds delineated with a 10,000 cells threshold with the 30 m DEM's available.
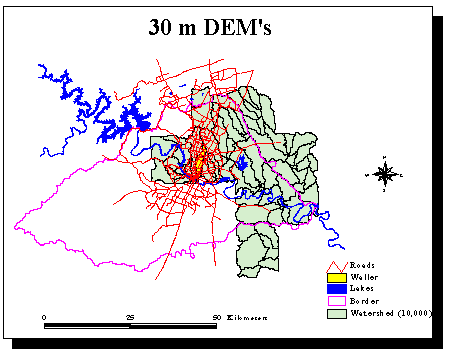
The 30 m DEM's improve greatly the delineation of Waller Creek watershed (in yellow on the previous map). The relative error between the observed and delineated areas drops to 0.5%.
A comparison between the delineation obtained with both types of DEM's shows the bigger accuracy of the 30 m DEM's, due to the smaller cell size.
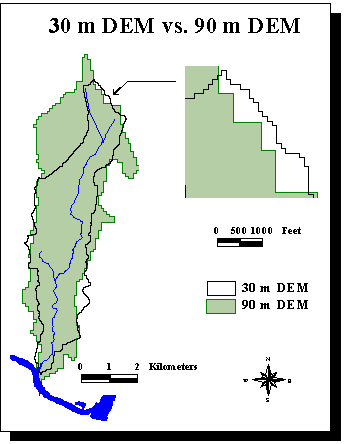
However, there are two principal drawbacks to use 30 m DEM's:
- they are more memory-consuming.
- the operations take longer.
The flow direction grid is based on the DEM's.
The DEM's have to be processed in order to be used in ArcInfo :
Description of Grid /DATABASES/AUSTIN/CHRISTINE/AUSTIN1
Cell Size = 30.000 Data Type: Floating Point
Number of Rows = 466
Number of Columns = 406
BOUNDARY STATISTICS
Xmin = 608085.000 Minimum Value = 130.000
Xmax = 620265.000 Maximum Value = 332.000
Ymin = 3346845.000 Mean = 213.601
Ymax = 3360825.000 Standard Deviation = 40.454
COORDINATE SYSTEM DESCRIPTION
Projection UTM
Zone 14
Datum NAD27
Zunits METERS
Units METERS Spheroid CLARKE1866
Parameters:
Example 2:
Arc: describe austin2
Description of Grid /DATABASES/AUSTIN/CHRISTINE/AUSTIN2
Cell Size = 30.000 Data Type: Floating Point
Number of Rows = 466
Number of Columns = 405
BOUNDARY STATISTICS
Xmin = 619965.000 Minimum Value = 555.000
Xmax = 632115.000 Maximum Value = 934.000
Ymin = 3360825.000 Mean = 779.027
Ymax = 3374805.000 Standard Deviation = 61.224
COORDINATE SYSTEM DESCRIPTION
Projection UTM
Zone 14
Datum NAD27
Zunits FEET
Units METERS Spheroid CLARKE1866
Parameters:
The grids must have the same characteristics to be merged together. Or the elevation values of the grids are
either in meters or in feet.
Convert all the grids to the same units (feet)
Arc: austin## = austin# / 0.3048 (Convert from meters to feet)
Merge the grids
Arc: grid
Grid: aus_utm = merge(austin11, austin2, ...)
Project in state plane coordinates
Grid: aus_st = project (aus_st, #, #, 100)
Project: output
Project: projection state
Project: zone 5376
Project: units feet
Project: parameters
Project: end
The value of the cell size after the projection is 100 ft.
The grid can then be displayed:
Arc: grid
Grid: display 9999
Grid: mape aus_st
Grid: gridpaint aus_st value linear nowrap gray

Burn in process
It consists in digging the stream network in the grid to be
sure the creeks are where
there are supposed to be. A digitized stream network is
used in the burn in procedure :
Convert the digitized network of the lakes and
of the creeks into two grids in state plane coordinates, and merge them together to create a grid of value 1.
Grid: lakes_gr = polygrid (lakes)
Grid: creeks_gr = polygrid (creeks)
Grid: water_gr = merge (lakes_gr, poly_gr)
Grid: streams = con (water_gr , 1)
Check that there is no gap in the streams.
All the gaps in the creeks must be filled (using Arctools), because one of the following procedure consists in
filling the sinks. The interruptions in a creek can prevent the water from flowing and this creek will then be considered as
a sink and filled.
The location of the creeks on the grid obtained with the DEM's must be the same as on the digitized grid. So "ditches" have to be digged in the DEM's at the locations of the streams. To reach this result, the elevations of the DEM'S are risen by adding 1000 ft to their
initial value.
Grid: aus_pls = aus_st + 1000
The DEM's raised 1000 ft are then merged with a grid (str_dem) containing the initial cells values for the streams and no data everywhere else. The result is a grid (burn_dem) where the streams keep their initial elevation values while 1000 ft
is added to every other cell.
Grid: str_dem = burn_crk * aus_st
Grid: burn_dem = merge (str_dem, aus_pls)
Flow direction computation
The sinks are filled in the burn in DEM to be sure that the water won't be
trapped but will be able to flow across the landscape.
Grid: fill burn_dem aus_fil SINK ausfdr (ausfdr is the grid
with the flow direction)
 Flow direction grid
Flow direction grid
The water flows from one
cell to its lowest neighbor along one of eight compass directions. Each cell is assigned a number corresponding to the direction of the cell with the steepest
descent.
East = 1 South-East = 2
South = 4 South-West = 8
West = 16 North-West = 32
North = 64 North-East = 128
The watersheds can be delineated in function of
the stream links or of the gage stations. Both delineations need to be made:
- the stream links watersheds are the ones for which the pollutants loading has to be evaluated.
- the stations watersheds are needed since
the discharge and concentration values are known at their oulet.
To delineate the watersheds, the stream network the computation
is based on must first be built.
The stream network is based on the flow accumlation grid obtained from the flow direction grid.
Grid: ausfac = flowaccumulation (ausfdr)
The stream network delineation depends on the choice of the threshfold used for flow accumulation.
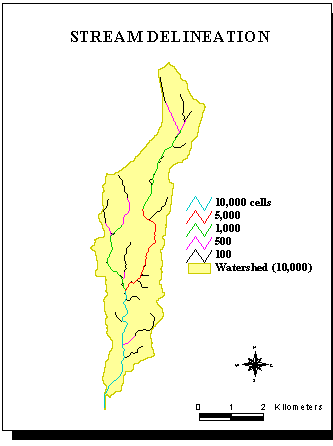
The streams are delineated by example for a 10,000 cells flow accumulation threshold.
Each cell has an area of 100*100 ft².
Grid: str10000 = con ( ausfac>10000 ,1 )
The grid can then be converted into a coverage.
Grid: stream10000 = streamline (str10000)
Each stream link of the stream network is separated:
Grid: link = streamlink ( str10000, ausdr)
The watersheds corresponding to these streamlinks are delineated using
the watershed function.
Grid: shd = watershed (aus_fdr, link)
This grid is then converted into a coverage:
Grid: wshed = gridpoly (shd)
There are two types of stations within the area of study.
- the USGS (US Geological Survey) stations
- the EII (Environmental Integrity Index) stations
There are 32 USGS stations within the area of study.
Their coordinates can be found in the USGS website
USGS Water Data for Texas .
There are 45 EII stations. Their locations have been determined
with a GPS system.
The coordinates of the stations are given in geographic degrees, minutes and seconds.
To be used to build the coverages, these data have first to be
converted into digital degrees :
Decimal Degrees (DD) = Degrees + Minutes/60 + Seconds/3600.
The west longitude is negative in decimal degrees.
The coordinates are put in a text file, stat.dat :
1 -98.0806 30.4208
2 -97.9078 30.3917
3 -97.7844 30.3719
4 -97.7861 30.3147
5 -97.9253 30.2961
...
end
The point coverages are build in Arc Info from the data in
a text file (e.g. stat.dat).
Arc: generate stations
Generate: input stat.dat
Generate: points
Generate: quit
Arc: build stations points
Arc: addxy stations
The result is a point coverage of the stations in geographic coordinates.
It has to be
projected to obtain a coverage in state plane projection,
which is the projection used for a study at
the scale of a city.
The input and output parameters of the projection from geographic to
state plane are written in a text file called sta_prj :
input
projection geographic
datum NAD27
units dd
parameters
output
projection state plane
zone 5376
datum NAD27
Zunits NO
Units FEET
Spheroid CLARKE1866
Xshift 0.0000000000
Yshift 0.0000000000
Parameters
end
The coverage stations in geographic coordinates
can now be converted into the coverage station
in state plane coordinates:
Arc: project cover stations station sta_prj #
AML (Arc Macro Langage) is the langage of programmation of Arc Info. Instead of having to type each time the commands step by step, AML enables to write a program which will do it automatically.
To build a point coverage, a AML called ptcov.aml is created in a text editor:
generate cover
input [response'name and path of the input file']
points
quit
build cover points
addxy cover
rename cover [response'name and path of the coverage']
&return
The program can be runned in Arc by using the AML command :
&run ptcov
It will prompt for the name and path of the input file and of the point coverage to create.
The stations should be located on the delineated creeks (the
digitized coverage is not accurate enough).
However, it is not always true and the errors have to be corrected. Arcview enables to check the location of the stations but it can not be used to do any modification. Only Arc Info enables to modify the data. The corrections can
be made in ArcTools, which can be accessed from Arc or from Grid (in this case, a grid must first be displayed using display 9999).
The coverages of the stations must first be converted into a grid (the grid str# of the stream network already exists):
Arc: Grid
Grid: station_gr = pointgrid (station)
Arcview is then used as a interface to display these grids
to check if the stations are located on the creeks.
If it is not true, then the grid must be
modified in order for the stations to be at the "right" place.
Once the grid with the stations is corrected, it is reconverted into a
point coverage:
Grid: station_sta = gridpoint (station_gr)
The two following shows the stations coverages built by this procedure:
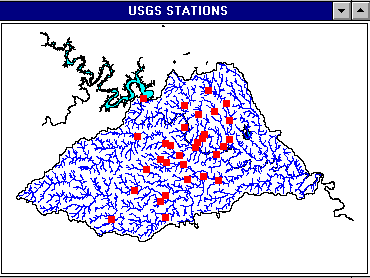
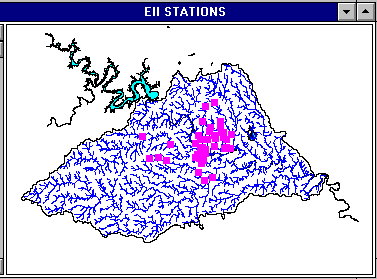
The point coverages of the stations must first be converted into grids which will be used
in the watershed function.
If EII_st is
the coverage of the EII station then the procedure is:
Grid: EII_gr = pointgrid ( EII_st )
Grid: EIIwshed_gr = watershed (ausfdr, EII_gr)
Grid: EII_wshed = gridpoly (EIIwshed_gr)
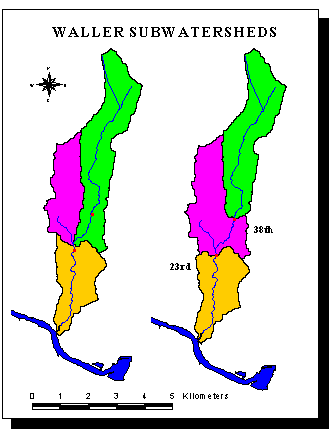
Here is a comparison between for Waller Creek. On the left are the subwatersheds obtained from stream links for a threshold of 1,000 cells. On the right the green area represents the drainage area for the station at 38th. The purple and the green are the drainage area for the station at 23rd.
A comparison between the USGS data for the drainage area of the 38th and 23rd stations and the values given by the GIS delineation (square miles) shows that the difference is less than 5%.
Stations 38th 23rd
USGS 2.31 4.13
30 m DEM 2.39 4.33
Error 3.5% 4.8%
Out of the 30 USGS stations in the area of study, 20 have
a period of record including at least one complete year. The period of record is based on water-years,
which start on October 1 and end on September 30. A water year is named by the year in which it ends.
For example, water year 1980 starts in October 1979.
The data for annual daily-mean discharge vary a lot from one year to another (e.g. from 1 to 7 cfs for Waller Creek at 23rd).
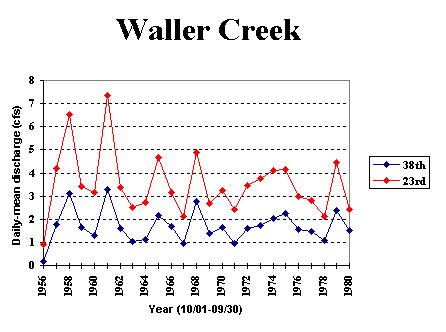
Can the prediction model be based on average values?
If we consider that pollutants concentrations are based only on the land use, then the pollution load for a given land use is directly proportionnal to the pollution load. In this case, using average values is not a good approach.
For the station at 23rd, the average annual daily-mean discharge is 3.5 cfs. For very wet years (discharge: 7cfs), the pollution loading is greatly under estimated (1/2 of the real load). On the other hand, for dry year (discharge: 1cfs), it is
highly over estimated (3.5 times).
It is then much more realistic to use a probability distribution to predict the discharge.
The pollutant load is defined as the product of the concentration by the discharge:
LOAD = Q * C
Hence
LN(Q*C) = Ln(Q) + Ln(C)
The concentrations C are lognormally distributed (they are defined by a median and a coefficient
of variation (CV)). Hence LN(C) is normally distributed.
A propriety of the normal distribution is that the sum of 2 normal distributions is
a normal distribution, whose
mean is the sum of the means and variance the sum of the variances.
If the discharge was lognormal (LN(Q) normal), the natural logarithm of the pollution
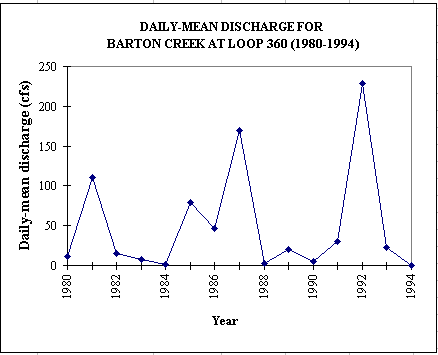
load would be the sum of 2 normal distributions, LN(Q) and LN(C). Or for a base period of 15 years (1980-1994), lognormal probability distributions
fit quite well the observed discharge data which are highly variable (2 orders of magnitude).
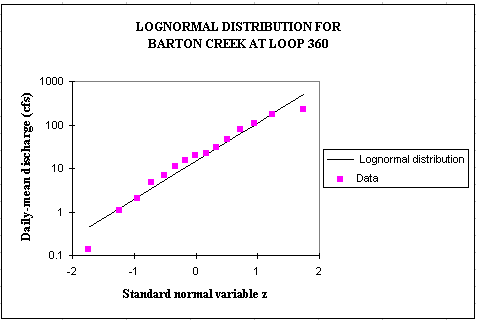
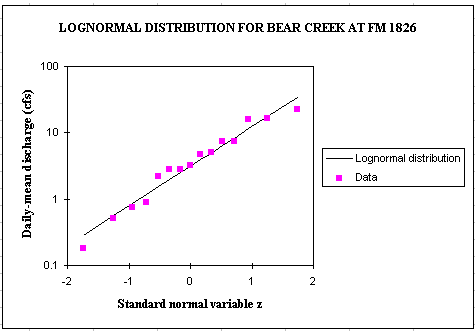
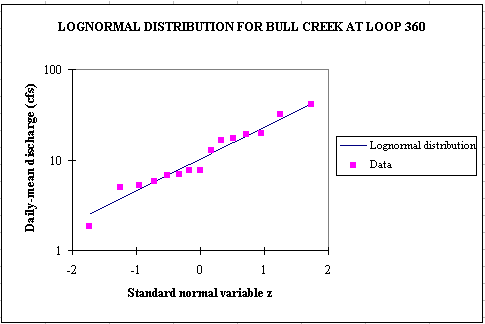
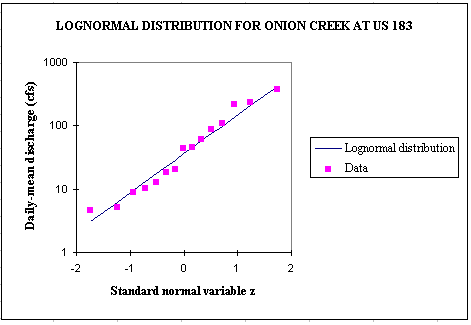
The following equations can then be used to compute the pollution load.
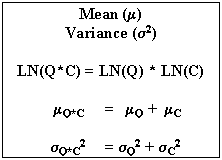
The parameters defining the concentration and the discharge are the median (50% probability)
and the coefficient of variation. Or the equations use the mean and the variance.
For a lognormal distribution, the mean and the variance can be obtained
from the median and the coefficient of variation by using the following relationships:
 The value corresponding to the equivalent
normal distribution are found by taking the natural logarithm.
The value corresponding to the equivalent
normal distribution are found by taking the natural logarithm.
The other component in the computation of the
rainfall runoff coefficient is the rainfall data. The annual average rainfall given by the City to use for loading calculations is 31.08 inches (after EPA procedures and the SYNOP program for hourly
data at the Austin airport for the period 1948-1993). Any "event"
that did not generate at least 0.05" of rainfall within 6 hours has been deleted.
The mean annual storm event is one that occurs, on average, 51.8 times a year, has a volume of .60", duration of 7.8 hours, average intensity of 0.106 inches/hour, and with 172.1 hours between storm even midpoints.
In Austin, it rains about every 7 days on average.
The discharge data are highly variable. Or they are directly related to the precipitation. A probability approach has equally to be used to determine the precipitation values which will serve as input to the model.
Precipitation data can be downloaded from the
National Climatic Data Center (NCDC) web site (3 stations for Austin).
To get the discharge from precipitation
values, some rainfall runoff relationships for every watersheds have to be established. These relationships will depend on
the land uses (related to impervious cover).
From the precipitation and discharge data a runoff coefficient, defined as the ratio of the discharge to the precipitation, can be found. For an
annual time scale, both contributions of base flow and direct runoff to the discharge are taken into account, so the base flow does not have to be substracted from the gauged streamflow.
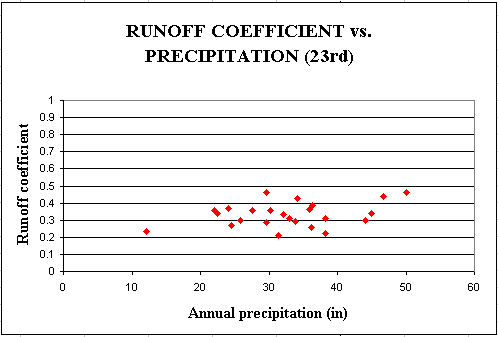
The following graph represent the variations of
the runoff coefficient for the drainage area of the USGS station at 23rd in Waller Creek watershed.
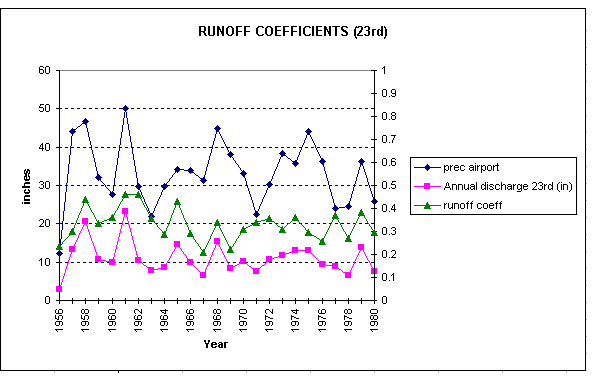
The runoff coefficient is in a range from 0.21 to 0.46 over a 24 year period with an average value of 0.33. The discharge, and then the runoff coefficient are related to the precipitation and to land use.
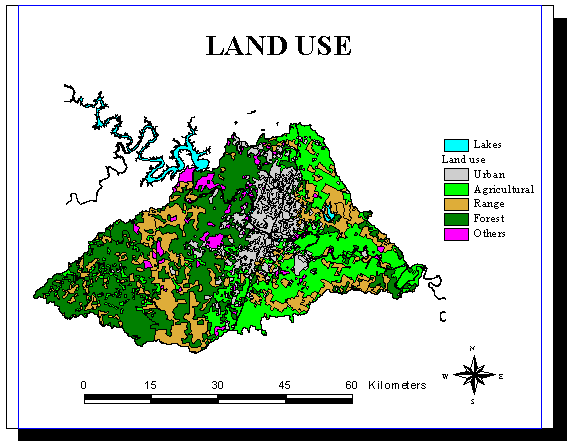
The Estimated Mean Concentration values are associated with
the land uses.
The land use coverage will be given by the City of Austin. It
will update the coverage of the Austin Spatial Database CDROM.
The categories used by the city of Austin are:
Current Impervious
Code Land Use Categories Cover Percentage
100 Single Family 30%-40%
-113 Mobile Home 30%-40%
200 Multi-Family 45%-80%
300 Commercial 60%-95%
400 Office 60%-95%
500 Industrial 60%-95%
600 Civic/Educational 30%-70%
700 Park 5%-15%
800 Transportation 85%-100%
-870 Utilities 25%-75%
900 Vacant/Undeveloped 5%-15%
-940 Water/Lake 100%
These impervious cover estimates are based on the assumption
that most streets and roads are included in the overall
land use they support. The streets of a Single Family
neighborhood are all included in the Single Family land
use along with the homes and yards, and not broken out separately.
The Transportation land use is reserved for only the largest of
roadways, such as IH-35 and MoPac,
or for other uses such as railroads, but not for average city streets.
Impervious Cover in Urban vs. Non-Urban Watersheds
For each land use category, the impervious cover is presented as a range.
In most cases this range is due to the different development
densities found in Austin. Single Family developments in
the central city tend to be more dense, and have more impervious cover,
than similar developments in more suburban areas.
It is recommended that in Austinís more urbanized watersheds,
land use categories be assigned impervious cover from the upper
end of the range. Conversely, in Austinís non-urban watersheds
values from the lower end of the range should be used.
Urban Impervious Non-Urban Impervious
Land Use Category Cover Estimate Cover Estimate
Single Family 40% 30%
Mobile Home 40% 30%
Multi-Family 80% 45%
Commercial 95% 0%
Office 95% 60%
Industrial 95% 60%
Civic/Educational 40% 40%
Park 15% 5%
Transportation 100% 85%
Utilities 50% 50%
Vacant/Undeveloped 15% 5%
Water/Lake 100% 100%
The grid is the product of the EMC grid by the rainfall runoff grid.
Grid: load_grid = EMC_grid*Runoff_gr
NPS pollution assessment for any point is done by using the weighted flow accumulation function.
Grid: NPS_grid = flowaccumulation (ausfdr, load_grid)
To observe the results:
Grid: display 9999
Grid: mape NPS_grid
Grid: gridpaint NPS_grid value linear nowrap gray
Grid: linecolor 4
Grid: arcs creeks
Grid: polygons lakes
Grid: cellvalue *
The NPS pollution load for any cell is obtained by clicking with the mouse on this particular cell.
The grid can then be converted into a coverage.
Grid: NPSint_grid = int (NPS_grid)
Grid: NPS_cov = gridpoly (NPSint_grid)
The coverage can be displayed in Arcview by adding the theme
NPS_cov. The repartition of the pollution load can be observed by choosing
some concentration ranges in the legend editor.
GIS is a very efficient tool for the assessment of nonpoint source pollution load. However, as natural phenomena such as precipitation (rather unpredictable) are involved, and
as there are not a lot of data available to build the model, NPS pollution load remains very difficult to evaluate accurately.
Go back to
my Home Page.