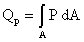The Niger River basin is a 2.3 million square kilometer area found between 5° N and 23° N of latitude, and 12° W and 17° E of longitude. The river rises in Guinea and flows for about 4,200 Km through Mali, Niger and Nigeria before reaching the Atlantic Ocean. Its main tributary, the Benue River, flows west from Cameroon and joins the Niger at Lokoja, Nigeria. In general, the basin landscape shows a great variability with desertic areas in the northern part and tropical areas in the south. The Inner Delta, just upstream of the city of Tombouctou in Mali, is a 150,000 Km² almost flat area with extremely high water losses due to evaporation, which makes it particularly difficult to model. Precipitation in the basin is also very variable, and it ranges from 2,700 mm/yr close to the river mouth to almost none in the desertic parts.

The model described here is a grid-based spatially-distributed mean-annual water balance model that uses time-averaged precipitation (in the form of grid) and flow at specific gauging stations (in the form of points) data, and topographic data (in the form of digital elevation model). After delineating the Niger river drainage area and determining the flow network within the basin (grid-cells connectivity), a relation between the potential flow Q_p (calculated as if all precipitation runoffs) and the actual flow Q_a is determined. This relation has the form Q_p = c Q_a, in which c is a runoff coefficient dependent on the precipitation in the drainage area, and allows one to estimate actual flow at any location of the basin.

Besides what is standard in a watershed delineation procedure (ESRI 1992, Meijerink 1994, Maidment 1995), for this particular case two additional goals had to be accomplished: (1) locate the streams so that the flow gauging stations lie on them; and (2) identify the pour point of the inland catchments (such as the Lake Chad basin).

To guarantee that delineated streams match observed streams and flow gauging stations, the DEM was corrected by increasing the elevation of all cells but the ones that coincide with the observed streams. This process is equivalent to dig trenches wherever a stream has been observed. This algorithm does not force the water to flow to the streams, but it does force it to remain in the streams once it gets in them. Hutchinson (1989) presents an algorithm to solve the problem of matching observed and modeled streams, that modifies the landscape model less than does the algorithm presented here. However, its implementation is more complicated.

The difficulty for delineating inland catchments is that the standard delineation procedure requires a depressionless DEM. Satisfying this requirement guarantees that the water is able to flow along the landscape without being trapped in depressions. The existence of DEM depressions is explained by pits (DEM errors that might be small but critical for hydrologic modeling), and by inland catchments (in which the lowest cell constitutes a pour point). Therefore, before delineating the streams, the DEM has to be corrected in the following ways: (1) filling the pits (for example, with the FILL function of Arc/Info-Grid), and (2) assigning a NODATA value to the lowest cell of the inland catchments (pour points).

The inland catchments problem is particularly important in the North-Western part of Africa, because it embodies two large terrain depressions: one is the Lake Chad basin; and the other comprises primarily the Algerian Sahara. Much attention has been paid to the Lake Chad basin because of its distinct hydrologic characteristics, i.e. the lake does not have an outlet river; on the contrary, the Algerian Sahara depression has not been given much importance because it is essentially a dry region.

The watershed delineation of the Niger River basin was based on the USGS digital elevation model of the African continent. This grid, originally in Geographic Projection with a cell size of 30 arc-seconds, was projected to Flat Polar Quartic Projection with cell size of 1000 m.

Given the mean-annual precipitation grid (Hutchinson, 1994), the mean-annual actual flow at the flow gauging stations (obtained from the Global Runoff Data Center in Koblenz, Germany), and the DEM, a methodology based on the runoff coefficient concept for determining the watershed contribution to the main stream was developed. This methodology considers that not all the water entering the system as precipitation flows to the main river, and that only a small fraction of the total precipitation does so, while most of it is lost as evaporation.

For determining the runoff coefficient, the following basic concepts were used:

• Potential flow Q_p (L³/T): is the maximum possible flow at a specific point of the catchment, and is equal to the total rainfall volume per unit time upstream of the point. It can be expressed as
  
  where P (L/T) is the spatially distributed mean-annual precipitation, and A (L²) is the drainage area. The integral can be understood as the volume under the precipitation P surface bounded by the drainage area A. The potential flow is a spatially distributed quantity and can be calculated, for example, with the Arc/Info-Grid function FLOWACCUMULATION with the mean-annual precipitation P grid as weight.

• Potential runoff R_p (L/T): is the average precipitation in the drainage area. The potential runoff is also a spatially distributed quantity and is calculated dividing the potential flow Q_p by the drainage area A, i.e. R_p = Q_p/A. The drainage area A is calculated with the Arc/Info-Grid function FLOWACCUMULATION without using any weight.

• Actual flow Q_a (L³/T): is the flow observed at the flow-gauging stations. The actual flow Q_a is defined only at the points where stations are located.

• Actual runoff R_a (L/T): is the portion of the potential runoff R_p that actually runoffs. As the actual flow Q_a, the actual runoff R_a is defined only at the points where stations are located. The actual runoff R_a is calculated dividing the actual flow Q_a by the drainage area A, i.e. R_a = Q_a/A.

Consequently, the runoff coefficient c is the ratio of the actual runoff R_a to the potential runoff R_p, giving c = R_a/R_p. The runoff coefficient c was estimated by means of an exponential regression that related the actual runoff R_a with the potential runoff R_p at the flow gauging stations (stations located on the main river were not considered for this regression).

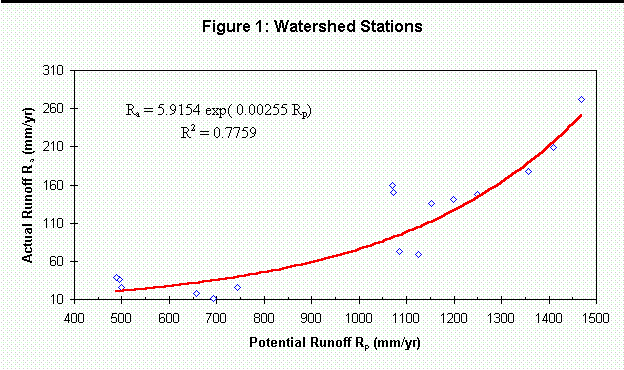
Figure 1 shows the analysis of the runoff coefficient for the Niger river basin. For values of the potential runoff R_p within the range 500-1450 mm/yr, it was found that R_a = 5.9154 exp(0.00255 R_p) with a regression coefficient r² = 0.78, which leads to

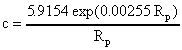( 1)

Out of the range indicated above, the runoff coefficient is uncertain. However, in order to match the observed flow at the stations upstream of the Inner Delta, it was assumed that c = 0.040 for R_p < 400 mm/yr, c = 0.400 for R_p > 1,900 mm/yr, and the interval of application of (1) was extended to 400-1900 mm/yr.

For a specific drainage area, which can be the total drainage area of a point or the incremental drainage area of a stream reach, the contribution of the watershed to the main stream flow Q_W is given by

( 2.a )

where A is the drainage area, or by

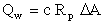( 2.b )

where A is the incremental drainage area of the reach. In equations (2), R_p represents the area-averaged precipitation in the drainage area (A or A whichever applies).

The mean-annual water balance of the Niger River main stream consisted in determining the flow longitudinal profile, i.e. the flow as a function of the river mile. For this purpose, the river was subdivided into 2,794 reaches (one reach per grid-cell of the main stream) and water balance was applied to each of them. The water balance equation for a reach is given by

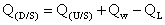( 3 )

which, in words, states that the flow at the downstream edge of a reach Q_(D/S) is equal to the flow at the upstream edge of the reach Q_(U/S), plus the inflow from the incremental drainage area of the reach Q_w, minus the water losses in the stream Q_L.

The water losses term Q_L is estimated using the actual flow at the main stream stations. For a river reach bound by two flow gauging stations, the water loss is given by

( 4 )

where Q_a(U/S) and Q_a(D/S) are the actual flow at the upstream and downstream stations. Finally, the water losses per unit length q_L are given by

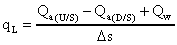( 5 )

where s is the reach length.

Table 1 shows how the water losses in the main stream were calculated. Only the river section between the stations of Koulikoro and Malanville were considered because those were the most upstream and downstream stations we had records of. Five river reaches, bound by six flow gauging stations (Koulikoro, KeMacina, Dire, Ansongo, Niamey and Malanville) were considered for the analysis. For each station, the river mile s, the drainage area A, the potential flow Q_p and the actual flow Q_a were determined. The river mile s was given by the flow distance from an arbitrarily defined river origin, in this case located 3300 Km from the ocean, and was calculated with the Arc/Info-Grid function FLOWLENGTH. For each reach, the length s, incremental drainage area A, incremental potential flow Q_p and incremental actual flow Q_a, were calculated as the difference between the downstream and upstream values. Next, the average precipitation in the incremental drainage area A of a reach, also called potential runoff R_p, was determined as R_p = Q_p/A. The watershed flow contribution to the river reach Q_w was calculated with equation (2.b) in which the runoff coefficient c was calculated with equation (1). Finally, the losses were determined with equation (4) or Q_L = Q_w - Q_a.

For the Niger river stream, because of the particular characteristics of the water losses in the Inner Delta area, two loss coefficients q_L were considered: one for the Inner Delta zone, and other for the rest of the river. For the Inner Delta zone, between the stations of KeMacina and Dire, it was found that the losses were 677 m³/s and the river length was 396 Km, which gives a loss coefficient q_L equal to 1.711 m³/s/Km. For the rest of the river, between Koulikoro (the most upstream station) and Malanville (the most downstream station), and excluding the Inner Delta, the losses were found to be 253 m³/s and the river length 1477 Km, giving a loss coefficient q_L equal to 0.171 m³/s/Km.

For determining the flow longitudinal profile, a procedure similar to the one presented above for the five reaches was applied. The only difference was that before (with the five reaches) the actual flow Q_a was known and the losses q_L were to be determined, while now (with 2,794 reaches) the losses q_L are known and the flow is to be determined.

For each of the 2,794 reaches, the river mile s, the drainage area A, and the potential flow Q_p were determined. Next, the length s, incremental drainage area A, and incremental potential flow Q_p, were calculated as the difference between the downstream and upstream values. The average precipitation in the incremental drainage area A of a reach, also called potential runoff R_p, was determined as R_p = Q_p / A. The watershed flow contribution to the river reach Q_w was calculated with equation (2.b) in which the runoff coefficient c was calculated with equation (1). Finally, the flow at the downstream end of the reach Q_(D/S) was determined with equation (3) where Q_L = q_L s. For these calculations, it was assumed that the flow at the upstream end of the reach Q_(U/S) was known, which implied that the process had to be applied downstream and that the flow at the river origin had to be calculated as the overland flow to that particular point.

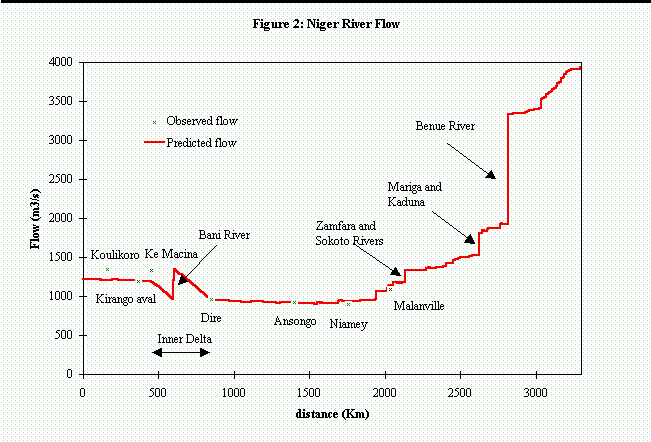
Figures 2 presents the flow longitudinal-profile Q vs. s, which shows a good fit with the observed flow in the stations. An overall water balance shows that out of 48,000 m³/s that enter the Niger River basin through precipitation, 42,900 m³/s (89%) are lost in overland flow and 1,100 m³/s (2%) in stream flow, leaving only 4,000 m³/s at the river mouth. This overall water balance does not account for actual water withdrawals separately, lumping them together with the losses.

The water balance of the Niger River was made with a grid-based spatially-distributed mean-annual hydrologic model. The main conclusions of this study can be summarized as follows:

1. Water losses in the watershed, due to evaporation, are much bigger than in the stream flow. This fact evidences the importance of understanding the physics of overland flow, although much more is known about stream flow.

2. The runoff coefficient c, used to evaluate the overland flow losses, was estimated as a function of the average precipitation in the drainage area R_p. For the Niger River basin, a strong correlation was found between the area-averaged precipitation and the runoff flow. A similar relation was found by Saunders and Maidment (1995) for the San Antonio-Nueces basin in Texas and by Olivera (1995) for the Souss basin in Morocco, although the catchment sizes were much smaller.

3. A methodology was developed for accounting for inland catchments. The Lake Chad basin and a depression in the Algerian Sahara were identified and delineated accordingly. The methodology consisted in asigning NODATA to the basin pour point, i.e. lowest DEM-cell of the depression, thus allowing water to drain out of the system.

4. Spatially-distributed hydrologic analysis can be done with GIS. Not only the analysis could be done, yet it would have been impossible to store and handle such amounts of information without GIS.

1. ESRI (1992), Cell-based Modeling with Grid 6.1: Supplement - Hydrologic and Distance Modeling Tools, Environmental Systems Research Institute (ESRI), Redlands, CA.

2. Hutchinson, M.F. (1989), A New Procedure for Gridding Elevation and Stream Line Data with Automatic Removal of Spurious Pits, Journal of Hydrology, No. 106, pp. 211-232, Elsevier Science Publishers B.V., Amsterdam.

3. Hutchinson, M.F, H.A. Nix, J.P. McMahon, K.D. Ord. (1994), A Topographic and Climate Database For Africa - Version 1, Center for Resource and Environmental Studies, Australian National University, Camberra ACT 0200, Australia.

4. Maidment, D.R. (1995), GIS & Hydrology, Workshop of the 15th Annual ESRI User Conference, May 21st, 1995, Palm Springs, California.

5. Meijerink, A.M.J., H.A.M. de Brower, C.M. Mannaerts and C.R. Valenzuela (1994), Introduction to the Use of Geographic Information Systems for Practical Hydrology, ITC, Publication Number 23, Enschede.

6. Olivera, F. (1995), Water Balance of the Souss Basin, University of Texas at Austin and United Nations Food and Agricultural Organization, http://civil.ce.utexas.edu/prof/maidment/olivera/morocco/report.htm

7. Saunders, W.K. and D.R. Maidment (1995), Grid-Based Watershed and Stream Network Delineation for the San Antonio-Nueces Coastal Basin, presented at Texas Water '95, August 14-18, 1995, San Antonio, Texas.