
October 1996
Prepared by David R. Maidment and Ferdi Hellweger
This exercise is intended to be performed with a Geographic Information System (GIS) program called ArcView. You may use any computer running ArcView 2.1 or later, UNIX based or PC. An introduction to ArcView exercise is available on-line and on the GISHydro97 CD rom.
In addition to ArcView you will need some programs developed by our research group. The programs are packaged in something called a project which you can load into ArcView like a file. You can download the project with the data.
The data consists of:
This exercise is concerned with visualizing and calculating data concerning atmospheric moisture flow over the Midwest during the period of the 1993 Midwest flood. The data were compiled into a database and interpolated onto the borders of the Midwest study region by Allan Bradley of the Iowa Institute of Hydraulic Research, to whom our gratitude is extended. He has provided the following explanation of how the data were developed:
The atmospheric water vapor fluxes were estimated from operational radiosonde data collected in the Midwest. Radiosondes are lanched twice-daily (0 and 12 UTC) to measure temperature, humidity, and wind profiles. For each radiosonde sounding, the vertically integrated fluxes was computed from the surface pressure (p_sfc) up to the top of the atmosphere (300 mb):

where:
qu is the flux in the x-direction,kg/m-s
qv is the flux in the y-direction,kg/m-s
u is the wind speed in the x-direction,m/s
v is the wind speed in the y-direction,m/s
q is the specific humidity,gm/gm
g is the accelaration of gravity,(9.81 m/s2) and
p is pressure, Pa.
The hydrostatic assumption is used to change from height coordinates z to pressure, therefore the - sign enters the equation. Also, the mass of water vapor is so small above 300 mb, integration beyond this point is unnecessary -- see Rasmusson, 1967, Atmospheric water vapor transport and the water balance of North America, Part 1, Characteristics of the water vapor flux field, Monthly Weather Review, 95(7), 403-426.
The flux estimates were then interpolated onto a 1 by 1 degree grid using a Barnes objective analysis (a standard meteorological method for interpolation). Bilinear interpolation was used to estimate the flux components onto the boundary points defined for the Midwest region.
Allen Bradley
University of Iowa
Institute of Hydraulic Research
404 Hydraulics Laboratory
Iowa City, IA 52242-1585
(319) 335-6117
(319) 335-5238 (FAX)
allen-bradley@uiowa.edu
The SAST study team defined the region of study below, which comprises all the drainage area of the Upper Mississippi River Basin and part of the Missouri River basin below Yankton, South Dakota. The drainage from western tributaries of the Missouri River, such as the Platte River and the Kansas River was cut off at gaging stations where the contributing flow from those drainage regions was known. The outlet of the study region is the Mississippi River at Thebes, Illinois, just upstream of the junction of the Mississippi and Ohio Rivers.
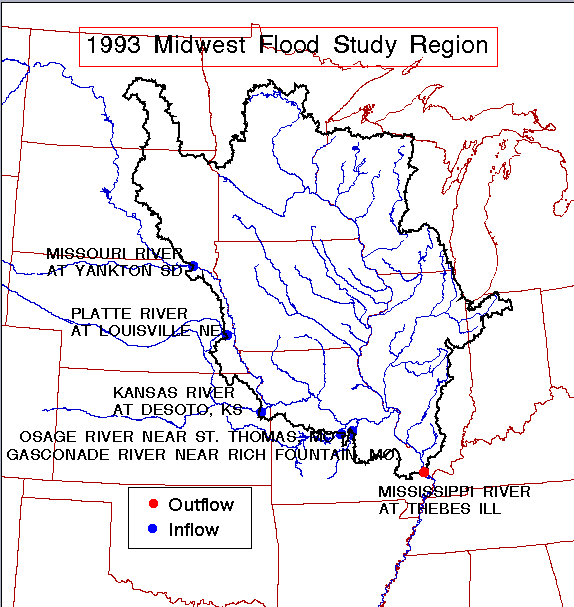
The boundary of this region was generalized by selecting a point each 100 km along the boundary and then joining these points by straight lines. Horizontal and vertical components of these lines in the S-N and W-E directions were formed by forming component lines in geographic coordinates (latitude-longitude) and projecting these into a Lambert Azimuthal Equal Area projection for the region. This map projection was chosen to preserve areas and the mutual relationship among the directions of the lines. The boundary line elements each have a From Node and a To Node at the ends where the direction of the nodes is arranged as being clockwise around the border of the study area. Here is a zoomed in view of the first boundary element. The length of the line is 61,684m, and its lx = 59,118m while its ly = 17,787 m. Note that squaring and summing the component lengths does not yield the square of the resultant length because in the projected planar domain, the components may no longer be mutually perpendicular as they are in geographic coordinates. The From Node of the line is located at (86.9954W, 41.5084N) and its To Node is located at (86.2849W, 41.6682N) where the longitudes (W) and latitudes (N) are given in decimal degrees.

The computation of the moisture flow rate across each line segment is
done using a vector cross product of the boundary line vector and the flux
vector.


In the example of the vectors shown, moisture flows into the region as
the product of the horizontal flux, qu, and the length over which it flows,
ly, and as the product of the vertical flux, qv, and the length over which
it flows, lx. Since lx (Eastward), ly (Eastward), and qu (Eastward) are
positive and qv (Southward) is negative, taking the sum (lx qv - ly qu)
ensures that both flow components are negative as required for them to
represent inflows. Similar diagrams can be drawn to show how the vector
cross product is computed for other boundary line segments.

The boundary lines are ordered clockwise, so that the interior of the region
is to the right and the exterior to the left of each boundary line. The
result of the vector cross product is a new vector pointing vertically
in the k direction, where upwards means positive mass flow, or mass leaving
the region, and downwards means negative mass flow, or moisture entering
the region. This sign convention is a standard fluid mechanics approach.
This exercise contains features showing the display of the flux field
for each 12 hour period and the flux computation around the boundary. The
map of the study region looks a bit flattened when compared to normal appearances
because it is presented in geographic, or latitude-longitude, coordinates.
Here is an example of the flux vectors computed at noon on 1 March 1993.

The necessary files to run this exercise are on the GISHydro97 CD rom in
the directory /atmos/atmobal.
Files:
atmobal.apr
qvfile.txt
qufile.txt
sastline.shp
sastline.shx
sastline.dbf
You can also get the files over the internet via ftp:
Address: ftp.crwr.utexas.edu
Login: anonymous
Password: your e-mail address
Directory: /pub/gishydro97/atmos/atmobal
Files:
atmobal.apr (binary)
qvfile.txt (ASCII)
qufile.txt (ASCII)
sastline.shp (binary)
sastline.shx (binary)
sastline.dbf (binary)
If you are new to ftp you might need instructions
on how to use anonymous ftp.
Start up ArcView and open the project ('atmobal.apr') from the file menu.
Look at the flux tables
The flux tables are called 'qufile.txt' and 'qvfile.txt'. The first
column stores the time. The following columns ('C1', 'C2', etc.) store
the moisture flux for the corresponding [kg/(m*s)]. Each row in the tables
stores the moisture flux representative of the time period.
Look at the line theme
The line theme is called 'sastline.shp'. It is displayed in a view
window called 'View1'. Click on the theme in the view's legend to make
it active. Then Click on the ![]() button on the tool bar. You can now get information on each of the lines
by clicking on them. When you click on a line ArcView looks up the matching
record in the themes attribute table and displays it. To view the entire
table select
button on the tool bar. You can now get information on each of the lines
by clicking on them. When you click on a line ArcView looks up the matching
record in the themes attribute table and displays it. To view the entire
table select ![]() from the 'theme'
menu.
from the 'theme'
menu.
Plot the flux vectors
Click on the ![]() button on the
views button bar to plot flux vectors. The program will ask you for any
data it needs in pop up windows. First, confirm that you will use the sastline
theme as the boundary line coverage:
button on the
views button bar to plot flux vectors. The program will ask you for any
data it needs in pop up windows. First, confirm that you will use the sastline
theme as the boundary line coverage:
Then specify which tables you will use to determine the qu and the qv components
of the flux:


Finally, specify what time point you wish to choose:

and the vectors will plot up on the screen. Pretty cool! Data are available
in the files supplied for this exercise at 12 hourly intervals from 1 March
thru 1 September 1993.
We expect to see strong atmospheric moisture flux on days with heavy rainfall. Here is the precipitation for the period March - August, 1993, for which the atmospheric moisture flow data are available.


Some of the most sustained rainfalls during the flood period occurred at the end of June and the beginning of July. Here is the flux field on July 5 at noon:

Click on the ![]() button on the views
button bar. Again, the program will ask you to supply the information it
needs, which is the name of the line theme, and the tables for qu and qv.
You will need to supply the name of a table for the results for which the
default is compflux.dbf. You can rename the compflux to anything you want
so long as it is 8 characters or less. You cannot create a compflux.dbf
table if one already exists so in that case choose another file name for
the results. As the program runs, a blue bar runs across the screen at
the bottom to indicate the progress of the computations. This calculation
takes a few minutes to be completed.
button on the views
button bar. Again, the program will ask you to supply the information it
needs, which is the name of the line theme, and the tables for qu and qv.
You will need to supply the name of a table for the results for which the
default is compflux.dbf. You can rename the compflux to anything you want
so long as it is 8 characters or less. You cannot create a compflux.dbf
table if one already exists so in that case choose another file name for
the results. As the program runs, a blue bar runs across the screen at
the bottom to indicate the progress of the computations. This calculation
takes a few minutes to be completed.
Look at the results table
Look at the results table, compflux.dbf If you didn't succeed
in getting a results table, or you can't get Arcview to run, you can pick
up a sample results table from the CD rom in /atmos/atmobal or by using
the same anonymous ftp address as at the beginning of this exercise (ftp.crwr.utexas.edu)
and you'll find a compflux.dbf file in /pub/gishydro97/atmos/atmobal. To
open the results table make the project window (atmobal.apr) active by
clicking on it. Click on the tables icon and then on the results table.
Click 'open' and ArcView will open the table. The units for the flux are
in 1,000,000,000,000 kg for each of the twelve hour periods.
The first five columns of the compflux.dbf table show:
Time: the date and time of the calculation in 12 hr increments.
Influx: the sum of the fluxes on the lines which have a net inflow
of atmospheric moisture to the region (taken as a positive number).
Outflux: the sum of the fluxes on the lines which have net outflow
to the region.
Netflux: Outflux - Influx, the net evaporation or precipitation
in the region.
Thruflux: (Outflux + Influx)/2, a measure of the rate of atmospheric
moisture flow over the region.
The flux values can be divided by the drainage area (698,525 km2) and by the water density (1000 kg/m3), and converted from units of 10^12 kg/12 hr into mm/12 hr. This computation can be done in Excel which imports the compflux.dbf file directly from Arcview. The resulting net flux and through flux are shown below:


You can see the periods of intense atmospheric flow in the through flux line. In the net flux line, the negative values indicate that inflow was greater than outflow, or that precipitation was greater than evaporation. The positive values indicate the reverse. As expected there are a majority of negative values, which contribute the moisture extracted from the air stream to supply precipitation during the flood.
Compute the flux for a line
Here is an example of the data needed to compute the flux across the
first boundary line (Line-id = 1) at noon on 1 March 1993:

You need the following data:
from the theme (sastline) attribute table:
lx = length of x component of line [m]. (59,118m)
ly = length of y component of line [m]. (17,787m)
The flux values are in columns where the label on each column is C followed
by the Line-id, e.g. C1 contains the data for Line-id = 1. Hence, from
the u flux table:
qu = moisture flux in the x direction [kg/(m*s)]. (114.96)
and from the v flux table:
qv = moisture flux in the y direction [kg/(m*s)]. (-53.60)
For the flux at noon on 1 March, 1993 in line number 1 (Line-id = 1), the
expression to be evaluated is:
Q = (lx qv - ly qu)
Hence, Q = (59118 x (-53.60) - 17787 x 114.96) = -5,213,518 kg/s. The total amount of moisture which flows over this boundary line in each 12 hour period is given by Q x 43,200, where 43,200 = 12 x 60 x 60, the number of seconds in 12 hours. Hence, the mass of moisture passing over this line in 12 hours on 1 March 1993 was -5,213,518 x 43,200 = -225,223,991,424 kg/12 hr. To make the numbers more readable, they are expressed in units of 10^12 kg/12 hr, so the flow presented in the compflux.dbf table is -0.2252 x 10^12 kg/12 hr. Again, the negative sign arises on this flux because it is an inflow to the region.
Wow! That seems like a lot of water. Lets see if this number makes sense. If we divide the mass flow rate 5,213,518 kg/s by the density of water (1000 kg/m3), we get the volumetric flow rate = 5,213 m3/s!!! For comparison, the maximum discharge of the Mississippi River near St Louis during the 1993 flood was 27,694 m3/s, so the flow of moisture across this boundary line is considerable, even when compared to the peak historical flood discharge of the largest river in the United States. And this boundary line is only one of 71 which make up the border of the drainage area.
During March, the atmosphere in the Midwest typically holds about 15 mm of water, so lets work out how fast this water is moving. One way of determining the velocity is to look at the moisture flux vector. This vector is (114.96, -53.60) kg/m-s and if we square and add the components the resultant flux is 127.31 kg/m-s. If this flux is divided by the density of water of 1000 kg/m3, the result is a discharge of 0.1273 m3/s of water per meter of land surface normal to the flow. If we further divide by a 15 mm estimate of the precipitable water in the atmosphere at this time, the result is an average moisture flow velocity of 0.1273/0.015 = 8.48 m/s, which is a reasonable number. So it appears that we really do have a vast river of moisture flowing over us in the atmosphere all the time.
A further calculation may serve to confirm this result. Suppose we take an atmosphere with 25 mm of precipitable water (the global annual average) and assume that the average velocity of movement is 5 m/s, then the discharge of water per meter width of flow is 5 x 0.025 = 0.125 m3/s per m, and to get a typical discharge in the Mississippi River at St Louis of say 10,000 m3/s requires 10,000 / 0.125 = 66666 m = 67 km or 43 miles width of atmosphere, about the distance between Austin and Johnson City. Wow, not very much! It is clear from these calculations that a great deal more water is flowing in the atmosphere than is flowing on the land surface, partly because in the atmosphere the water vapor can flow everywhere unimpeded while on the land surface the flow paths of streams and rivers are restricted to a very small part of the landscape.
The coincidence between the periods of negative net atmospheric moisture
flux and precipitation can be examined by summing the net atmospheric moisture
flux for each 12 hourly period to give daily totals and plotting those
alongside the concurrent precipitation over the region. The result shows
a remarkably good agreement as to the timing of periods of precipitation
being nearly always associated with negative atmospheric moisture flow.
The rather high positive atmospheric moisture flow during dry periods suggests
that when precipitation ceases, evaporation increases significantly.

The evaporation can be estimated by using the relation:
Evaporation = Net Atmospheric Moisture Flux + Precipitation
Doing this on a daily basis produces a rather erratically fluctuating evaporation with negative values one day followed by positive values the next. This is not surprising, bearing in mind the fact that the net atmospheric moisture flux is found as the difference between two much larger quantities, the moisture inflow and outflow to the region so it contains all the random errors associated with the computation of the moisture flow. Never the less, the average evaporation from 1 March to 31 August so determined is found to be:
Evaporation (2.28mm) = Net Flux (-1.93mm) + Precip (4.21 mm)
and the ratio of evaporation/precipitation = 2.28/4.21 = 54%, approximately the same ratio as that found in the surface water balance study.
If 10-day averages of precipitation and evaporation are taken, it appears
that periods of high precipitation are followed by periods of high evaporation
as the weather clears and the region dries out. Evaporation appears to
be suppressed during sustained periods of high precipitation, such as that
which occured during June and the early part of July.

These materials may be used for study, research, and education, but please credit the authors and the Center for Research in Water Resources, The University of Texas at Austin. All commercial rights reserved. Copyright 1997 Center for Research in Water Resources.