Prepared by Christine Dartiguenave and David R. Maidment
To use Geographic Information System to compute the mean precipitation over a given area by the Thiessen method, the Inverse Distance Weighting Method and the Spline Method. The problem solved is from the textbook Applied Hydrology, by V.T.Chow, D.R. Maidment, and L.W. Mays, McGraw-Hill, 1988, problem #3.4.5. The basic idea of the problem is to determine the mean areal precipitation over a watershed given the precipitation values at gages within and around the watershed. The shape of the watershed is simplified and the data are hypothetical, but they are representative of the problem as encountered in practical situations.
This exercise is intended to be performed with Geographic Information System (GIS) programs Arc/Info version 7.0 or later, and Arcview, version 2.1 or later.
This exercise is concerned with computing the mean precipitation over an area. It is possible to do it by hand but it is less time-consuming and easier to do it with GIS (once you know how to do it).
Open text editor and create first a file called gages .dat that includes the gage sequence and the (x,y) coordinates of each gage. Your file should look like this :
1 7 4 2 3 4 3 -2 5 4 -10 1 5 -3 -3 6 -7 -7 7 2 -3 8 2 -10 9 0 0 endDon't forget to type 'end' (and press return).
Then create a file called prec.dat that includes the gage sequence and the corresponding values of precipitation recorded. It should look like this :
1 62 2 59 3 41 4 39 5 105 6 98 7 60 8 41 9 81 endAnd don't forget to type end.
Finally you have to create a file called border.dat for the polygon coverage of the border of the area.
1 0 0
5 5
-5 5
-5 -5
0 -10
5 -5
5 5
end
end
The first line indicates the number of the polygon and the spatial
coordinates of its label point (0 0).
In general, it is the center of the polygon.
The succeeding lines contain the coordinates of the vertices of the polygon and
you finish by typing the same vertex you began with (5,5), which shows
that a polygon is formed as a closed set of vertex points.
You write end to indicate the end of the polygon 1, and end again to
indicate the end of the file.
Start up Arc, and then type:
Arc: generate gages
Generate: input gages.dat
Generate: points
Creating points with coordinates loaded from gages.dat
Generate: quit
Externalling BND and TIC...
arc: build gages points
Building points...
arc: addxy gages
Adding X,Y Coordinates to gages.PAT
Now we have a coverage with no attribute data in it. To attach the precipitation data to the point coverage follow the steps below. First, create a template for the attribute table pprecip.dat by defining its fields and their names :
Arc: tables
Enter Command: define pprecip.dat
1
Item Name: gages-id
Item Width: 4
Item Output Width: 4
Item Type: i
2
Item Name: prec
Item Width: 6
Item Output Width: 6
Item Type: n
Item Decimal Places: 2
Item Name: [just hit return here to indicate
end of table definition]
Next, add the data into this table from the text file:
Enter Command: add from prec.dat
Real value expected.
Don't worry about this statement -- eveything
still works fine, with this error
Enter Command: q
Leaving TABLES...
Now, join the data table pprec.dat to the point coverage of the gage locations gages, by using the gages-id as the key field to link gage locations with the precipitation measured at each gage.
Arc: joinitem gages.pat pprec.dat gages.pat gages-id
gages-id
Joining gages.pat and pprec.dat to create gages.pat
This command joins the point attribute table of your point coverage, gages.pat, with the precipitation data table you just created, called pprec.dat. The new table will also be called gages.pat, the relate items is the gages-id field and the prec data will be placed after the gages-id field.
Now, before going further, check that you have entered all the data correctly.
Arc:list gages.pat gages-id, x-coord, y-coord, prec
Record gages-id x-coord y-coord prec
1 1 7.000 4.000 62.00
2 2 3.000 4.000 59.00
3 3 -2.000 5.000 41.00
4 4 -10.000 1.000 39.00
5 5 -3.000 -3.000 105.00
6 6 -7.000 -7.000 98.00
7 7 2.000 -3.000 60.00
8 8 2.000 -10.000 41.00
9 9 0.000 0.000 81.00
arc:thiessen gages thies
Loading points from coverage gages...
Triangulating...
Creating Thiessen Structure...
Constructing arc/polygon Topology...
Generating polygon attributes....
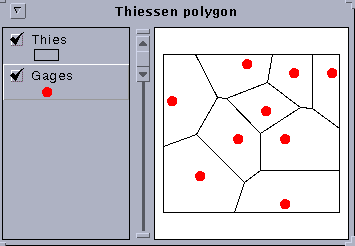
Now, start up arcview to see how it looks. Open a new view and in the view window click on add theme gages for the point coverage and thies for the Thiessen polygon. Here is the result. Wow! Looks pretty cool!

Start up Arc, and then :
Arc: generate border
Generate: input border.dat
Generate: polygons
Creating polygons whith coordinates loaded from border.dat
Generate: quit
Externalling BND and TIC...
arc: build border polygons
Building polygons...
arc: addxy border
Adding X,Y Coordinates to border.PAT
Now go to arcview and add border as a theme. We have now to get rid of what is not in the border to get the areas inside.
arc: clip thies border area
Clipping thies with border to create area.
Sorting...
Intersecting...
Assembling polygon...
Creating new labels...
Creating / / / AREA.PAT
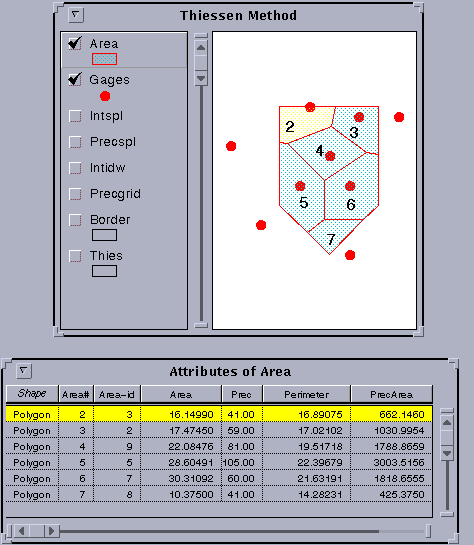
You can do that with Arcview.
Click on :
view/start editing

edit/add field
You will get the window Field Definition :
Name : PrecArea
Type : Number
Width : 16
Decimal Places : 4
Then press OK.
Click on the left icone under table to select all records
in your table.
Then click on the field calculator just under help.
You will see the Field Calculator Window. Select Area
then press return, select
the star (to multiply), press return, select
prec, and press return. Click on OK.
Then go to field/statistics...
You will have the statistics for the PrecArea field whose sum is 8729.5534
Then select the field Area in the table and get the statistics for this field.
The total area is 125.
Divide 8729.5534 by 125 and you will find the mean precipitation
which is 69.84 mm.
Arc: grid
Grid: setcell .1
Grid: precgrid = idw ( gages, prec )
Running ... 100%
Grid:display 9999
Grid: mape precgrid
Grid: gridpaint precgrid
Now you can see what you just created.
You can now go to Arcview and add precgrid as a theme.
This time it is a image data source.

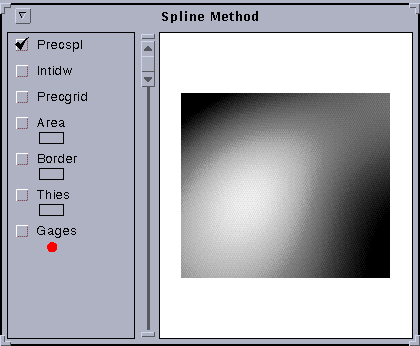
You can see some circles in this map. These are produced by the idw method around particular gage values, something like the high point of a circus tent at the point where it is held up by a center pole, or the reverse for a gage with a low data value. This local peak and valley appearance may be appropriate for precipitation over a short time interval during a storm but it is probably not appropriate for long-term mean precipitation. Later, an alternative method called Spline is used to smooth out these peaks and pits in the precipitation map.
Now, lets compute the mean precipitation over the watershed. This is done by creating a mask grid with values only in the watershed area within the border coverage. The Grid function Zonalmean determines the average of the values of the precipitation surface within the watershed mask zone.
Start up Arc again and type:
Arc: grid
Grid: borgrid = polygrid (border)
Converting polygons from BORDER to grid BORGRID
Number of Rows = 150
Number of Columns = 100
Percentage of Gridded Cells...100%
Grid: mnidw = zonalmean (borgrid, precgrid)
Percentage of Cells Processed:100%
Grid: Describe mnidw
Description of Grid / / /MNSPL
Cell Size = 0.100 Data Type: Floating Point Number of Rows = 151 Number of Columns = 171 BOUNDARY STATISTICS Xmin = -10.050 Minimum Value = 69.654 Xmax = 7.050 Maximum Value = 69.654 Ymin = -10.050 Mean 69.654 Ymax = 5.050 Standard Deviation = 0.000 NO COORDINATE SYSTEM DEFINEDThe mean precipitation this method is 69.65 mm.
If you want to keep just the area within the border, type :
Grid: intidw = con ( borgrid > 0 , precgrid )
Running ... 100%
And then add this theme in arcview.

You can see the circles around the highs and lows in the gage values more easily in this picture.
The procedure is quite similar to that for inverse distance weighting.
Arc: grid
Grid: setcell .1
Grid: precspl = spline ( gages, prec )
Running ... 100%
Grid: display 9999
Grid: mape precspl
Grid: gridpaint precspl
you can add the theme precspl.
Grid: mnspl = zonalmean (borgrid, precspl)
Percentage of Cells Processed:100%
Grid: Describe mnidw
Description of Grid / / /MNIDW
Cell Size = 0.100 Data Type: Floating Point Number of Rows = 151 Number of Columns = 171 BOUNDARY STATISTICS Xmin = -10.050 Minimum Value = 70.572 Xmax = 7.050 Maximum Value = 70.572 Ymin = -10.050 Mean 70.572 Ymax = 5.050 Standard Deviation = 0.000 NO COORDINATE SYSTEM DEFINEDThe mean precipitation by this method is 70.57 mm.
If you want to keep just the area within the border, type :
Grid: intspl = con ( borgrid > 0 , precspl )
Running ... 100%
And go to arcview to add this theme.
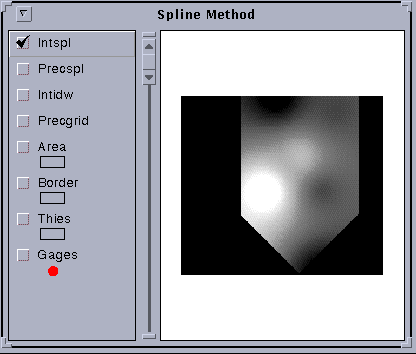
Pretty cool!
Ok, this exercise is done. Please clean up by deleting all the files and coverages you created while doing it.