by David R. Maidment, Francisco Olivera,
Seann Reed, Zichuan Ye, Sandra Akmansoy and Daene C. McKinney
Center for Research in Water Resources
University of Texas at Austin
The FAO/UNESCO Water Balance of Africa is an effort undertaken jointly by the Center for Research in Water Resources (CRWR) of the University of Texas at Austin, the United Nations Food and Agriculture Organization (FAO), and UNESCO, for the purpose of better assessment and planning of the water resources of Africa. The Water Balance of the Niger River Basin is a pilot study for which the map-based methodology of soil-water, surface-water and groundwater balance has been developed. The Niger basin was studied because the basin is not providing enough food for its population, and water resources development programs are being considered as a means of improving the availability of water for food production. Evaluating such programs requires assessment of the amount and spatial pattern of available water resources, and the impact of development projects upon them. The water balance model is developed to help with these tasks. Data files for application of this model at any location of the earth have been compiled into a Digital Atlas of the World Water Balance, presently being prepared in CD-ROM format.
Monthly soil water surplus is calculated using the Thornthwaite soil water balance model in which the evaporation computation has been modified to include a spatial database of net radiation obtained from the Earth Radiation Budget Experiment. These water surpluses are transferred onto subwatersheds and routed using a subwatershed response function for the flow within a subwatershed, and the Muskingum method for the river flow downstream of the subwatersheds. The flow from the subwatershed to the river moves partly by subsurface flow, and partly by surface flow, each flow being delayed in time by a differing amount depending on whether it is surface or subsurface flow.
The Niger River basin is a 2.3 million square kilometer area located between 5° N and 23° N of latitude, and 12° W and 17° E of longitude. The Niger River rises in Guinea and flows for about 4,200 Km through Mali, Niger and Nigeria before reaching the Atlantic Ocean at the Gulf of Guinea. Its main tributary, the Benue river, flows west from Cameroon and joins the Niger at the city of Lokoja, Nigeria. The basin landscape shows great variability, with desert areas in the northern part and tropical areas in the southern part. Precipitation ranges from 2,700 mm/yr close to the river mouth to almost nothing in the desert, and most precipitation occurs during an annual monsoon period between July in September, which results in an annual flood that takes several months to propagate down through the river network. Just upstream of the city of Tombouctou in Mali, the Inner Delta of the Niger River is located, a huge shallow depression which fills and empties each year as the annual flood passes through, and results in about half the inflow being lost to evaporation.
Stream-watershed delineation is the process of identifying the flow elements (streams) and contributing areas (watersheds) of a hydrologic system. It is assumed that the flow is essentially channel flow in the streams and overland flow in the watersheds. A stream is initiated on the DEM where the upstream drainage area exceeds a user-defined threshold value, and watershed boundaries are delineated from outlets at each stream junction, which produces a drainage network with a single stream for each watershed.
The procedure for delineating streams and watersheds from DEM's requires a depressionless DEM. Satisfying this requirement guarantees that the water flows along the landscape without being trapped in depressions. The existence of DEM depressions is explained by inland catchments, but also by DEM errors or pits (which might be small for most practical purposes but critical for hydrologic modeling) . Inland catchments are hydrologic systems that drain towards an inland pour point located within the basin, and not on the basin border as usually occurs. Thus, inland catchments do not drain towards the oceans as most systems do. On the other hand, pits produce unreal termination of drainage paths and alter substantially the stream network. Therefore, it is essential to correct the DEM errors by filling the pits prior to delineating the streams and watersheds. Arc/Info-Grid includes the FILL function which can be used to fill the DEM depressions up to a level in which they can drain towards the main stream network. However, this procedure makes no difference between actual and fictitious terrain depressions, and fills them all without discerning between DEM errors and inland catchments. Actual terrain depressions should be kept in the DEM as part of the terrain definition. In brief, correcting the DEM consists of (1) defining the internal pour points of the inland catchments ( i.e., assigning NODATA value to the lowest cell of each depression), and (2) filling the pits with the FILL function, so that the water can flow towards the stream network or pour points without being trapped in the depressions.
The DEM correction required a criterion to distinguish between DEM errors and actual terrain depressions. The criterion adopted was that a sink is an actual terrain depression if its filled areas is greater than a threshold area and and its filled depth is greater than a threshold depth defined by the user. For this purpose, an Arc Macro Language (aml) that applies this criterion automatically and corrects the DEM was developed. The methodology used by the program to identify inland catchments consists in filling the DEM and comparing the area and depth of the filled zones with certain user-defined threshold values. All filled zones that satisfy the criterion are treated as inland catchments and NODATA is assigned to their lowest cell (pour point) in the original DEM. Once all the pour points have been assigned NODATA, the DEM is filled with the FILL function to correct the pits. After the DEM is corrected, the standard stream and watershed delineation process can be used.
The North-Western part of the African continent embodies two large terrain depressions: one is the Lake Chad basin, and the other comprises primarily the Algerian Sahara. Much attention has been paid to the Lake Chad basin because of its distinct hydrologic characteristics (i.e., the lake does not have an outlet river); on the contrary, the Algerian Sahara depression is essentially a dry region.
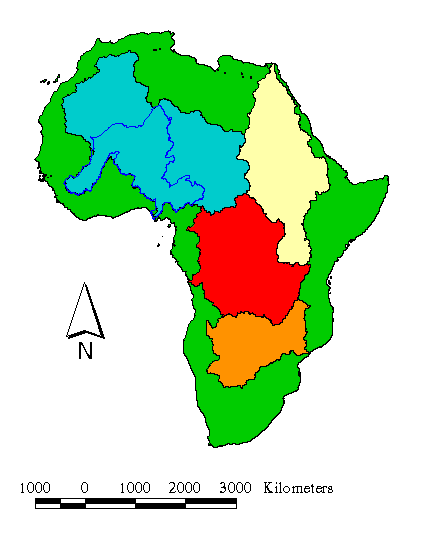
The following figure shows the watersheds that drain more than 1,000,000 Km2 of Africa delineated before identifying the inland-catchment pour points. In this map, the yellow area corresponds to the Nile River basin, the red to the Congo River basin, the orange to the Zambezi River basin, and the light blue area to the Niger River basin (including the actual Lake Chad basin and part of the Sahara desert). The delineation of these watersheds was based on the DEM prepared by M.F. Hutchinson of the Center for Resource and Environmental Studies (CRES) of the Australian National University. This DEM, originally in Geographic Projection with cell size of 3 arc-minutes, was projected into Flat Polar Quartic (FPQ) Projection with cell size 5000 m. After correcting the DEM for inland cathments, a new watershed delineation was done which solved the problem of areas draining towards the Niger river. The border of the actual Niger River basin is outlined in dark blue in the map below.

The stream-watershed delineation of the Niger River basin was based on the DEM of the African continent developed by the EROS Center of United States Geological Survey (USGS) in Sioux Falls, South Dakota, with the cooperation of the United Nations Environment Program (UNEP). This DEM is part of a global DEM file called GTOPO30. This DEM grid, originally in Geographic Projection with a cell size of 30 arc-seconds, was projected into FPQ Projection with cell size 1000 m. Next, a smaller area that comprised North West Africa (approximately 12.3 million Km2) was clipped out and taken as the study area.
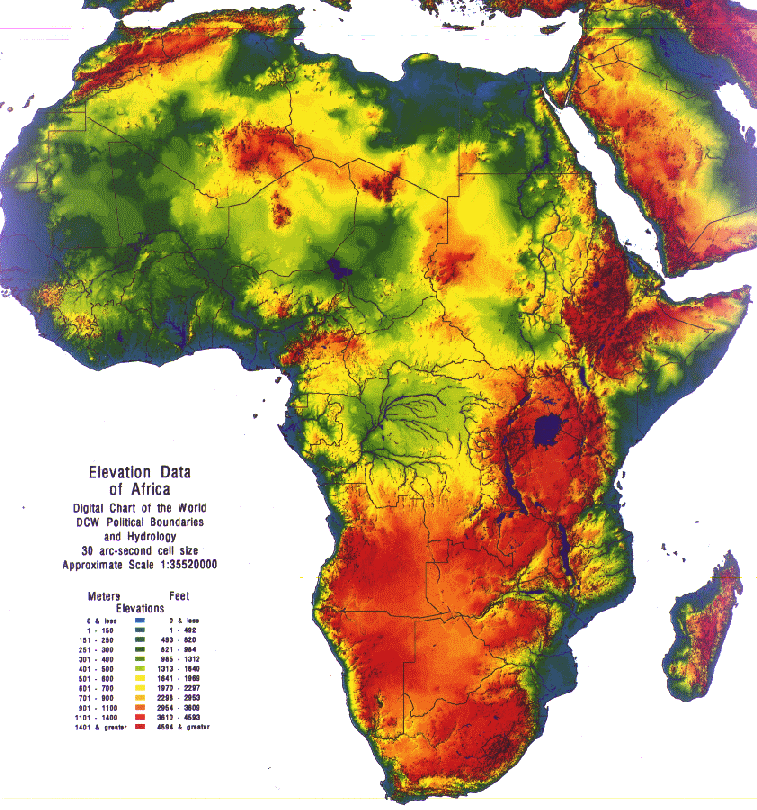
It was found that the Niger River basin has an area of approximately 2.3 million square kilometers. Using a threshold drainage area of 10,000 Km2 for the delineation of the sub-watersheds, a total of 142 stream-watershed units were identified. The threshold drainage area of 10,000 Km2 was chosen in order to obtain a number of stream-watershed units large enough to preserve the spatial variability of the system, and small enough not to complicate the calculations. Additionally, in order to avoid extremely long subwatersheds, watershed outlets were also placed each 250 Km along the main stem of long rivers within a single subwatershed, which added 25 new stream-watershed units. The resulting stream lengths ranged from 1 Km to 250 Km with an average value of 117 Km, and the watershed areas ranged from 16 Km2 to 66,430 Km2 with an average value of 14,000 Km2. The following figure shows the stream-watershed units of the Niger River hydrologic system.
Mean monthly temperature and precipitation estimates interpolated onto
a 0.5 by 0.5 mesh were obtained from Cort Willmott at the University of
Delaware. These data come from the Global Air Temperature and Precipitation
Data Archive compiled by D. Legates and C. Willmott. The monthly precipitation
estimates used in this study were corrected for gage bias. Data from 24,635
terrestrial stations and 2,223 oceanic grid points were used to estimate
the global precipitation field. The climatology is largely representative
of the years 1920 to 1980 with more weight given to recent ("data-rich")
years (Legates and Willmott, 1990). The raw data obtained from the University
of Delaware were downloaded via ftp in formatted text files. FORTRAN programs
and AML's were used to generate the polygon coverages of these data, shown
here below.
Global mean monthly net radiation data generated as part of the International Satellite Cloud Climatology Project (ISCCP) are now available for a 96 month period extending from July 1983 to June 1991. The data are given on the ISSCP equal-area grid which has a spatial resolution of 2.5 degrees at the equator. Monthly average, mean annual and mean monthly values of net radiation were computed for this 8 year period. To make computations consistent, the radiation data were resampled to the same resolution as the climate and soils data (0.5 degree cells).
The formula used for computing the potential evaporation is the Priestley-Taylor equation:
where E is the potential evaporation rate in mm/month, D is the gradient of the saturated vapor pressure curve in kPa/°C at the prevailing temperature, g is the psychrometric constant in kPa/°C, and Er is the water evaporation equivalent of the net radiation in mm/day. The values of D and g as a function of temperature are given in Table 4.2.1 p. 4.4 of the Handbook of Hydrology, (McGraw-Hill, 1993, ed. by D.R. Maidment). The value of Er is given by:
where Rn is the net radiation in W/m2, L is the latent heat of vaporization of water in J/kg, and 86,400 is the number of seconds in a day. The value of L is given by:
where T is the prevailing temperature.
Global estimates of "plant-extractable" water capacity - also called soil water-holding capacity - on a 0.5° grid estimates were obtained via anonymous ftp from the USGS Geophysical Fluid Dynamics Laboratory. Information about sand, clay, organic content, plant rooting depth, and horizon thickness was used to estimate the water-holding capacity. An important source of data used in this analysis was FAO's Digitized Soil Map of the World (FAO, UNESCO, 1974-1981). As a reference, the global average soil water-holding capacity estimate is 86 mm.
The soil-water balance model uses a simple accounting scheme to predict soil-water storage, evaporation, and water surplus. Surplus is precipitation which does not evaporate or remain in soil storage and includes both surface and sub-surface runoff. The conservation of mass equation for soil-water can be written as follows (Thornthwaite 1948):
where w is soil moisture, t is time, P is the precipitation, E is the actual evaporation, and S is the water surplus.
An Avenue script (Reed 1996), based on WATBUG (Willmott 1977), is used to calculate the soil water budget. The actual calculations are done on a daily basis in the program. Values of the monthly precipitation and potential evaporation are divided by the number of days in the month to give average daily values. The runoff or water surplus in each day is found as the product of the precipitation and the ratio of the actual soil moisture level to the soil moisture capacity. The evaporation in each day is found as the product of the potential evaporation and the ratio of actual soil moisture level to the soil moisture capacity. A trial calculation is done to find the end of day storage and if this exceeds the soil moisture capacity, the excess soil moisture is added to the water surplus and the storage is reset to the soil moisture capacity before the next day's computations are done. This algorithm is limited by the fact that it assumes that a month's rain falls as a gentle mist instead of in concentrated daily amounts with zero rainfall in between. This simplification is offset by allowing a small amount of runoff or water surplus in each day, as occurs with a soil slowly draining to a stream. The algorithm used here can also be applied with daily data files when such data are available and then its daily results are more realistic.
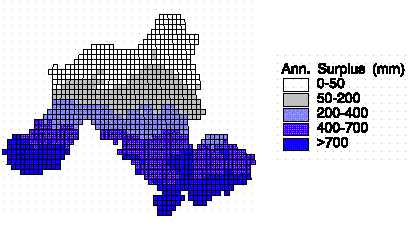
The climate data used are mean monthly values for the period of record. The computations are done for the12-month representative period several times in sequence, until the computed soil moisture levels in each month stabilize to constant values. These values represent expected monthly soil moisture levels. The annual water surplus for each 0.5° by 0.5° cell are shown in the figure:
Avenue scripts are also used to run a map-based surface water simulation model of the Niger River basin. After delineating the stream-watershed network, so that a one-to-one relation between stream and corresponding drainage area is established, water is routed to each subwatershed outlet assuming overland flow and next it is routed through the stream system. Overland flow within the subwatersheds is modeled with a response function, equivalent to the instantaneous unit hydrograph. Stream flow in the river network is modeled with the Muskingum method or a response function.
Water losses in the overland flow are assumed to be proportional to the flow distance from each specific elementary area (grid cell) to the subwatershed outlet. The constant of proportionality is found by calibration, by comparing mean annual predicted flows with observed flows at eleven flow gauging stations distributed over the watershed, and is given by
where a is the constant of proportionality, Qobs is the observed flow, S is the spatially distributed mean annual surplus, L is the distance to the subwatershed outlet, and A is the station drainage area.
In Arc/Info-Grid, the flow length grid L was determined with the FLOWLENGTH
function; and the terms
and
were calculated
with the ZONALSTATS function applied to the S (mean annual
surplus) and S L (product of mean annual surplus and flow length) grids.
The calculated values of a (one per station) varied from 0.0010/Km to 0.0035/Km,
with an average value of 0.0028/Km and standard deviation of 0.0009/Km.
From the physical point of view this implies that, as an average, 0.28%
of the surplus is lost per kilometer of overland flow. This water losses
parameter is applied uniformly over the entire watershed.
Concluding, net surplus S'i(t) (i.e. the fraction of surplus that is not lost) in subwatershed i is given by
where Lo i is the average overland flow length to the subwatershed outlet.
Inputs to the surface and shallow subsurface water systems of subwatershed i are fractions of the net surplus S'i(t). Splitting the net surplus into surface and subsurface surplus is made by a uniformly distributed factor a. Spatial variability of this factor is a matter of further research. Two impulse response functions are defined, one for the surface system ui(t) and another for the subsurface system vi(t). Each of them is used to route the fraction of the surplus that feds each system.
Surface System: A smoothed time-area diagram of the subwatershed is used as the impulse response function. For calculating the flow time, a spatially distributed velocity field in which the local velocities are proportional to the square root of the terrain slope and the drainage areas is assumed. The proportionality factor ai becomes a calibration parameter. However, since getting the time-area diagram for each of the subwatersheds would be tedious specially if a large number of subwatersheds are considered, the diagram is represented by two numbers: (1) average flow time Ti; and (2) standard deviation si. Based on these two numbers, an impulse response function ui(t) in the form of a first passage times distribution is assumed
where Di plays the role of a diffusion number. Using this flow-time distribution has the following advantages: (1) the flow is represented in a form that has been used previously in the literature for modeling water flow; (2) a smooth response instead of an irregular curve is obtained; (3) the response is defined by two numbers and one formula, instead of a list of values.
Shallow Subsurface System: The watershed response function is assumed to be an exponential distribution
where ki is the distribution parameter. The physical meaning of this assumption is that underlying each subwatershed, a linear reservoir is located. This reservoir stores the water for a relatively long time before releasing it to the subwatershed outlet. The linear reservoir is defined by it residence time ki, which is the only calibration parameter of the shallow subsurface system response. The reservoir residence time is taken as a function of the subwatershed area.
Overall Subwatershed Response: The flow at the subwatershed outlet is calculated as the sum of the surface and the shallow subsurface system responses. Each response is the result of the convolution of its corresponding surplus fraction and its impulse response function
where a is the surface/subsurface spliting factor. After reaching the subwatershed outlet the flow is routed in the stream network
Depending on the flow time in the stream, flow is modeled by either method: (1) Muskingum method; or (2) response function. In order to reduce the number of model parameters, stream flow velocity is taken constant as v =0.3 m/s. Moreover, losses are represented by a loss coefficient that is the flow lost per unit flow per unit length. The loss coefficient is taken equal to 0.114*10-6/m everywhere but in the Inner Delta where it is 1.41*10-6/m.
For the Muskingum method, the parameters K (flow time in the reach) is taken equal to L / (1.67 v) where L is the reach length and X is taken equal to 0.1.
For the response function method, a response has to be defined by the user for the reach as a series of values. For short streams in which the flow-time in the reach is in the order of magnitude of the time-step, a 2-time-step response function method is suggested. The 2-time-step response function is based on the fraction of the flow that reaches the downstream edge of the stream before one time step, the remaining being the value of the response function for the first time step. The 2-time-step model is the default model, and is implemented when a user-defined response function is not available or when the Muskingum method is not computationally efficient.
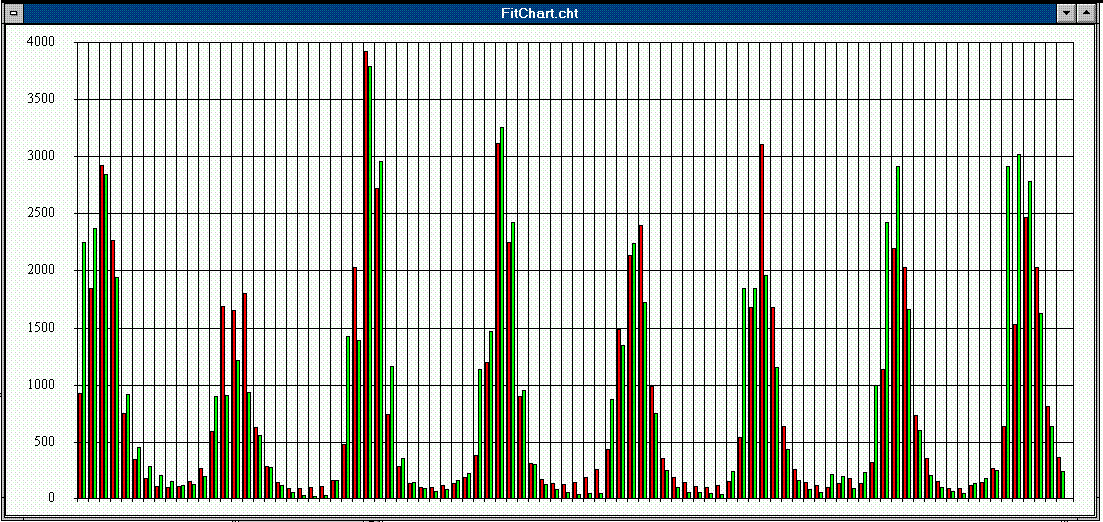
The graphics attached depict the simulated and observed flow for the Niger river at Koulikoro, one of the principal gaging stations on the Niger river above its Inner Delta.
The results are obtained by clipping out a portion of the main basin model to form the Koulikoro submodel, including just those subwatersheds whose drainage passes through the gage at Koulikoro. Next, the model parameters are optimized so that the predicted discharge at the station matches observed values.
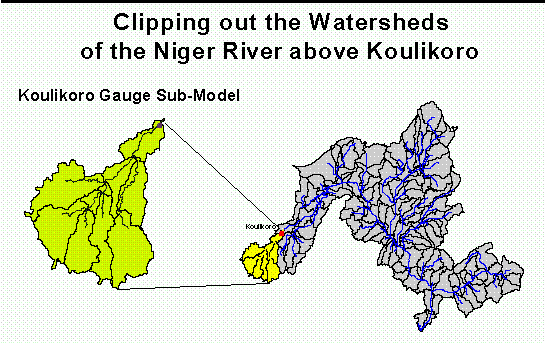
The simulations carried out are for a 90 month period from July 1983 to December 1990. In the attached chart, the horizontal axis is the time in months from July 1983, the vertical axis is the Niger River discharge in cubic meters per second, the green lines are the calculated flows and the red lines are the observed flows at Koulikoro. The observed flow data were obtained from the Global Runoff Data Center in Koblenz, Germany.
The Water Balance of the Niger Basin project accomplished several goals:
The project demonstrated the flexibility of the Avenue programming language but we also learned that Avenue programs are not suited to computationally intensive tasks because they take too long to execute.
We wish to acknowledge the support and cooperation of the Land and Water Development Division of the UN Food and Agriculture Organization (Jean-Marc Faures and Philippe Pallas) and the Division of Water Sciences of UNESCO (Alice Aureli) in the conduct of this study.
Legates, D.R., and C.J. Willmott (1990), "Mean Seasonal and Spatial Variability in Gauge-Corrected Global Precipitation", International Journal of Climatology, 10, 111-127.
Reed S. (1996), "Soil-Water Budget. Part I: Methodology and Results", http://www.ce.utexas.edu/prof/maidment/GISHydro/seann/explsoil/method.htm
Thornthwaite, C.W. (1948), "An Approach Toward a Rational Classification of Climate", Geographical Review, 38, 55-94.
Willmott, C.J. (1977), "WATBUG: AFORTRAN IV Algorithm for Calculating the Climatic Water Budget", Publications in Climatology, 30, 2.
United Nations - Food and Agriculture Organization (1994), "Digitized Soil map of the World", Version 3.0.
These materials may be used for study, research, and education, but please credit the authors and the Center for Research in Water Resources, The University of Texas at Austin. All commercial rights reserved. Copyright 1997 Center for Research in Water Resources.