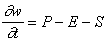 (4.1)
(4.1)
The soil-water balance model uses a simple accounting
scheme to predict soil-water storage, evaporation, and water surplus.
Surplus is precipitation which does not evaporate or remain in
soil storage and includes both surface and sub-surface runoff.
The conservation of mass equation for soil-water can be written
as follows:
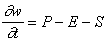
In Equation 4.1, S is surplus, P is precipitation,
E is evaporation, w is soil moisture, and t is time. Horizontal
motion of water on the land surface or in the soil is not considered
by this model. Snow melt was also not considered in these computations,
but this probably does not introduce significant error for a study
in Texas. Willmott et al., 1985, describe a simple scheme that
could be included to account for snow melt.
At first glance, it would seem that the most natural
spatial unit to use in a soil-water balance would be a soil map
unit, but these map units have very irregular shapes and a wide
range of sizes. Because climate data also play an important role
in the soil-water balance, the cells generated when climate data
are interpolated onto regular grids are a judicious choice for
use as the modeling units in the soil-water balance. Climate
data interpolated onto 0.5 grid boxes are used in this study.
A major source of uncertainty in evaluating Equation
4.1 is estimating the evaporation. Estimation of evaporation is
based upon knowledge of potential evapotranspiration, water-holding
capacity of the soil, and a moisture extraction function. These
concepts and a method for evaluating Equation 4.1 are described
below. Special consideration of the potential evapotranspiration
concept is provided in Section 4.2.
4.1.2 Description of
input data
4.1.2.1 Climate data
Global data sets of mean monthly temperature and precipitation interpolated to a 0.5°
grid were obtained from an anonymous File Transfer Protocol (ftp) server to the University of Delaware (climate.geog.udel.edu). These data are from the "Global Air Temperature and Precipitation Data Archive" compiled by D. Legates and C. Willmott. The precipitation estimates were previously corrected for gage bias. Data from 24,635 terrestrial stations and 2,223 oceanic grid points were used to estimate the precipitation field. The climatology is largely representative of the years 1920 to 1980 with more weight given to recent ("data-rich") years (Legates and Willmott, 1990).
4.1.2.2 Water-holding
capacity data
Global estimates of "plant-extractable water capacity" have recently become available on a 0.5°
grid (Dunne and Willmott, 1996). As used in this report, the term plant-extractable water capacity is equivalent to available water-holding capacity. One reason given for developing this global database was to eliminate the need for assuming spatially invariant plant-extractable water capacity in soil-water balance computations made over large areas. Information about sand, clay, organic content, plant rooting depth, and horizon thickness was used to estimate the plant-extractable water capacity. Figure 4.1 shows the distribution of this parameter throughout Texas. The global average for this parameter is 86 mm while the average in Texas is 143 mm.
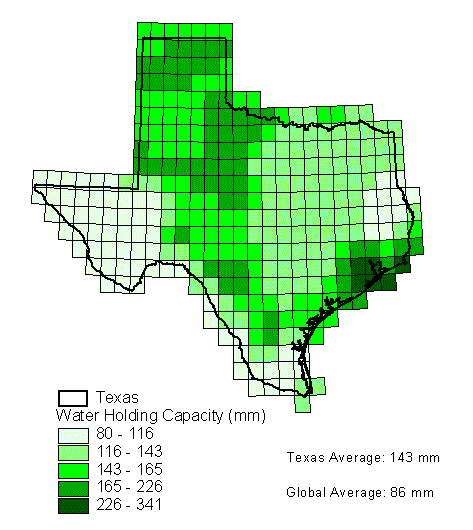
4.1.2.3 Open Water Evaporation
Estimates
Estimates of open water evaporation based upon pan
evaporation measurements were provided by Alfredo Rodriguez at
the Texas Water Development Board (TWDB, 1995). The data consist
of monthly average gross reservoir evaporation estimates for one
degree quadrangles in and around Texas. Monthly data for 1940
to 1990 are available in 75 quadrangles thoughout Texas and monthly
data for 1971-1990 in an additional 28 quadrangles at the border
of Texas. Mean monthly values were computed from these data and
used for estimates of potential evaporation in the soil-water
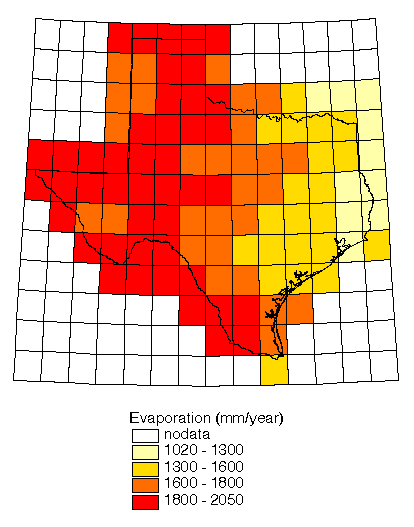
balance calculations. Figure 4.2 shows the one degree quadrangle
index map, shaded to indicate where data are available. Figure
4.3 shows mean annual reservoir evaporation. As an alternative,
a global radiation data set described in the next section has
recently become available that facilitates making potential evaporation
estimates using the Priestley-Taylor equation. This method was
also considered for use in the soil-water balance computations.
An insightful comparison of these two methods for estimating
potential evapotranspiration is described in Section 4.2.
A global radiation data set recently made available
makes using the Priestley-Taylor method a feasible option for
estimating potential evapotranspiration in large scale studies.
These data are described by Darnell et al., 1995, and
were obtained by anonymous ftp to cloud.larc.nasa.gov. The data
set includes longwave and shortwave radiation flux estimates for
a 96 month period extending from July 1983 to June 1991. The
data are given on the ISSCP equal-area grid which has a spatial
resolution of 2.5 at the equator. Darnell et al., 1992,
describe advances in input data and flux estimation algorithms
that improve the ability to assess the radiation budget on a global
scale. Input data improvements have come from the International
Satellite Cloud Climatology Project (ISCCP) and the Earth Radiation
Budget Experiment (ERBE). Using this satellite data, the radiation
budget components that cannot be measured directly are estimated
independently using physical approaches that have been validated
against surface observations. According to Darnell et al.,
1995, longwave flux estimates fall within +/- 25 W/m2
of surface measurements while Whitlock et al., 1995, estimate
the accuracy of shortwave estimates to be within +/- 20 W/m2
of surface measurements. For comparison, the energy required to
evaporate 1 mm/day of water is about 30 W/m2. In this
study, net radiation (equivalent to net shortwave + net longwave)
is used.
4.1.3 Water-holding capacity
of the soil
In order to calculate the soil-water budget, an estimate
of the soil's ability to store water is required. Several terms
are used by soil scientists to define the water storage capacity
of soils under different conditions. The field capacity or drained
upper limit is defined as the water content of a soil that has
reached equilibrium with gravity after several days of drainage.
The field capacity is a function of soil texture and organic
content. The permanent wilting point or lower limit of available
water is defined as the water content at which plants can no longer
extract a health sustaining quantity of water from the soil and
begin to wilt. Typical suction values associated with the field
capacity and wilting point are -10 kPa (-0.1 bars) and -1500 kPa
(-15 bars) respectively. Like water content, field capacity and
permanent wilting point are defined on a volume of water per volume
of soil basis. The water available for evapotranspiration after
drainage ( or the available water-holding capacity ) is defined
as the field capacity minus the permanent wilting point. Table
4.1 gives some typical values for available water-holding capacity.
Table 4-1 : Typical Values for Soil-water
Parameters by Texture*
| Texture Class | Field Capacity | Wilting Point | Available Capacity |
| Sand | 0.12 | 0.04 | 0.08 |
| Loamy Sand | 0.14 | 0.06 | 0.08 |
| Sandy Loam | 0.23 | 0.10 | 0.13 |
| Loam | 0.26 | 0.12 | 0.14 |
| Silt Loam | 0.30 | 0.15 | 0.15 |
| Silt | 0.32 | 0.15 | 0.17 |
| Silty Clay Loam | 0.34 | 0.19 | 0.15 |
| Silty Clay | 0.36 | 0.21 | 0.15 |
| Clay | 0.36 | 0.21 | 0.15 |
*Values obtained from ASCE, 1990, Table 2.6, p.21.
For budgeting calculations, it is useful to know
the total available water-holding capacity in a soil profile.
This value is typically expressed in mm and can be obtained by
integrating the available water-holding capacity over the effective
depth of the soil layer. A one meter soil layer with a uniform
available water-holding capacity of 0.15 has a total available
water-holding capacity of 150 mm. For the remainder of this paper,
the term water-holding capacity means total available water-holding
capacity in units of mm. The water-holding capacity is denoted
with w* and the current level of moisture storage in the soil
is denoted by w [mm]. A large water-holding capacity implies
a large annual evapotranspiration and small annual runoff relative
to a small water-holding capacity under the same climatic conditions.
4.1.4 Estimating Actual
Evapotranspiration
To estimate the actual evapotranspiration in the
soil-water budget method many investigators have used a soil-moisture
extraction function or coefficient of evapotranspiration, f,
which relates the actual rate of evapotranspiration to the potential
rate of evapotranspiration based on some function of the current
soil moisture content and the water-holding capacity.
Dyck, 1983, Table 1, (reprinted in Shuttleworth, 1993, Table 4.4.6) provides a summary of some moisture extraction functions used by different investigators. Mintz and Walker, 1993, Figure 5, also illustrates several moisture extraction functions. Many researchers agree that soils show the general pattern of behavior that moisture is extracted from the soil at the potential rate until some critical moisture content is reached when evapotranspiration is no longer controlled by meteorological conditions. Below this critical point, there is a decline in soil moisture extraction until the wilting point is reached. This type of behavior is illustrated by Shuttleworth, 1993, Figure 4.4.3, p. 4.46 and Dingman, 1994, Figure 7-21. Shuttleworth, 1993, notes that the critical moisture content divided by the field capacity is typically between 0.5 and 0.8. The type of moisture extraction function just described is commonly applied to situations when daily climate data are used. A function in which the ratio of evapotranspiration to potential evapotranspiration is proportional to the current moisture level, f = w/w*, has been applied when budgeting with monthly climate values and this function is used here. This function predicts lower evapotranspiration rates than a function with a breakpoint which may offset (to some degree) the low rainfall intensities resulting from the use of monthly averaged rainfall. (4.2)
4.1.5 Budgeting soil moisture to yield surplus
Soil-water budget calculations are commonly made
using monthly or daily rainfall totals because of the way data
are recorded. Computing the water balance on a monthly basis
involves the unrealistic assumption that rain falls at constant
low intensity throughout the month, and consequently surplus estimates
made using monthly values are typically lower than those made
using daily values. In dry locations, the mean potential evaporation
for a given month may be higher than the mean precipitation and
budgeting with monthly values may yield zero surplus, even though
there is some observed runoff. For this reason, the use of daily
values is preferred over monthly values when feasible, yet daily
budgeting still does not adequately describe storm runoff that
occurs when the precipitation rate exceeds the infiltration capacity
of the soil. One drawback to using daily data is that it is difficult
to interpolate daily rainfall over space. For the statewide study
undertaken here, the use of daily data was deemed too cumbersome.
Equation 4.3 describes how soil moisture storage
is computed.
if wi < w*
Si = wi - w* and set wi
= w* if wi > w* (4.3)
In Equation 4.3, wi is the current soil
moisture, wi-1 is the soil moisture in the previous
time step, P is precipitation, PE is potential evapotranspiration,
Si is the surplus in a given day, f is the soil-moisture
extraction function and w* is the water-holding capacity. With
monthly data, computations are made on a quasi-daily basis by
assuming that precipitation and potential evapotranspiration for
a given day are equal to their respective monthly values divided
by the number of days in the current month. When evaluating Equation
4.3, if wi drops below zero, then wi is
set equal to 0.01; if wi > w*, then the surplus
for that day is wi-w* and wi is set equal
to w*. The soil-moisture extraction function f =w/w* was
used for this study.
If the initial soil moisture is unknown, which is
typically the case, a balancing routine is used to force the net
change in soil moisture from the beginning to the end of a specified
balancing period (N time steps) to zero. To do this, the initial
soil moisture is set to the water-holding capacity and budget
calculations are made up to the time period (N+1). The initial
soil moisture at time 1 (w1) is then set equal to the
soil moisture at time N+1 (wN+1) and the budget is
re-computed until the difference (w1 - wN+1)
is less than a specified tolerance.
4.2 Potential Evapotranspiration
One aspect of the soil-water budget that involves
significant uncertainty and ambiguity is estimating potential
evapotranspiration. Just the concept of potential evapotranspiration
is ambiguous by itself, as discussed in the next section. Two
potential evapotranspiration estimates were considered for this
study, gross reservoir evaporation estimates from pan coefficients
and estimates made using the Priestley-Taylor equation. As discussed
later, the gross reservoir evaporation estimates are considered
to be better than the Priestley-Taylor estimates for use in the
soil-water budget calculations.
4.2.1 Potential evaporation
vs. potential evapotranspiration
Thornthwaite, 1948, first used the concept of potential
evapotranspiration as a meaningful measure of moisture demand
to replace two common surrogates for moisture demand, temperature
and pan evaporation. Potential evapotranspiration refers to the
maximum rate of evapotranspiration from a large area completely
and uniformly covered with growing vegetation and with an unlimited
moisture supply. There is a distinction between the term potential
evapotranspiration and potential evaporation from a free
water surface because factors such as stomatal impedance and plant
growth stage influence evapotranspiration but do not influence
potential evaporation from free water surfaces.
Brutsaert, 1982, notes on pp. 214 and 221 the remarkable
similarity in the literature among observations of water losses
from short vegetated surfaces and free water surfaces. He poses
a possible explanation that the stomatal impedance to water vapor
diffusion in plants may be counterbalanced by larger roughness
values. Significant differences have been observed between potential
evapotranspiration from tall vegetation and potential evaporation
from free water surfaces. The commonly used value of 1.26 in
the Priestley-Taylor equation was derived using observations over
both open water and saturated land surfaces. For the most part,
the term potential evapotranspiration will be used in this paper
and, as used, includes water loss directly from the soil and/or
through plant transpiration.
An additional ambiguity in using the potential evapotranspiration
concept is that potential evapotranspiration is often computed
based on meteorological data obtained under non-potential conditions
(Brutsaert, p. 214). In this study, temperature and net radiation
measurements used for calculating potential evapotranspiration
in dry areas and for dry periods will be different than the values
that would have been observed under potential conditions. The
fact that the Priestley-Taylor method exhibits weak performance
at arid sites is related to this ambiguity because the assumptions
under which the expressions were derived break down. This is
particularly relevant to West Texas and is the main reason why
evaporation estimates derived from pan coefficients are considered
more applicable for the type of computations being made in this
study. A comparison of the two methods is described in Section
4.2.3.3.
Although not used directly in this study, a brief
review of the widely used Penman equation serves as a good starting
point for discussing the estimation of potential evapotranspiration.
4.2.2 Penman combination
method
Two requirements for evaporation to occur are an
energy input and a mechanism for the transport of water vapor
away from the saturated surface. In light of this, two traditional
approaches to modeling evaporation are an energy budget approach
and an aerodynamic approach. With the energy budget approach,
the net radiation available at the surface (shortwave radiation
absorbed less longwave radiation emitted) must be partitioned
between latent heat flux and sensible heat flux, assuming that
ground heat flux is negligible. This partitioning is typically
achieved using the Bowen ratio which is the ratio of sensible
heat flux to latent heat flux. Approximating the Bowen ratio
typically requires measurements of temperature and humidity at
two heights. The aerodynamic approach involves a vapor transport
coefficient times the vapor pressure gradient between the saturated
surface and an arbitrary measurement height. Determination ofthe vapor transport coefficient requires measurements of wind
speed, humidity, and temperature. Brutsaert, Chow et al.,
and Dingman, present equations for calculating the Bowen ratio
and vapor transport coefficients. Without simplifying assumptions,
energy budget and the aerodynamic methods require meteorological
measurements at two levels.
In 1948, Penman combined the energy budget and aerodynamic
approaches. Penman's derivation eliminates the need for measuring
water surface temperature; only the air temperature is required.
The resulting equation is as follows:
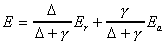
where Er = 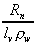
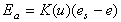
The Penman equation is a weighted average of the
rates of evaporation due to net radiation (Er) and
turbulent mass transfer (Ea). Provided that model
assumptions are met and adequate input data are available, various
forms of the Penman equation yield the most accurate estimates
of evaporation from saturated surfaces. The "Evapotranspiration
and Irrigation Water Requirements Manual," ASCE, 1990, offers
a performance comparison of twenty popular methods for estimating
potential evaporation. The top six rated methods in ASCE, 1990,
are forms of the Penman equation (p.249).
Two simpler methods that are much easier to apply
than forms of the Penman equation were considered in this study,
a pan coefficient approach and the Priestley-Taylor method.
Evaporation pans are commonly used to estimate open
water evaporation from nearby lakes and reservoirs. The rate
of evaporation is estimated by measuring the change in water level
with time. Lake evaporation is estimated by multiplying the pan
evaporation by a pan coefficient. Typical values of the pan coefficient
range from 0.67 to 0.78 in Texas, so the measured evaporation
from the pan is higher than that from the lake surface. Pan coefficients
vary with location and season. The development of gross reservoir
evaporation estimates used in this study is described by TWDB,
1995. As discussed in Section 4.2.1, open water evaporation and
potential evapotranspiration are often of similar magnitude, justifying
the use of open water evaporation estimates in soil-water budget
calculations.
4.2.3.2 Priestley-Taylor
Method
In 1972, C.B. Priestley and R.J. Taylor showed that, under certain conditions, knowledge of net radiation and ground dryness may be sufficient to determine vapor and sensible heat fluxes at the Earth's surface. When large land areas (on the order of hundreds of kilometers) become saturated, Priestley and Taylor reasoned that net radiation is the dominant constraint on evaporation and analyzed numerous data sets over land and ocean to show that the advection or mass-transfer term in the Penman combination equation tends toward a constant fraction of the radiation term under "equilibrium" conditions. According to Brutsaert, 1982, Slatyer and McIlroy, 1961, first defined the concept of equilibrium evaporation as a state that is reached when a moving air mass has been in contact with a saturated surface over a long fetch and approaches vapor saturation thus causing the advection (aerodynamic) term in the Penman equation to go to zero. Both the Slatyer-McIlroy and the Priestley-Taylor definitions consider the radiation term in the Penman equation to be a lower limit for the evaporation from a moist surface. The form of the evaporation equation developed by Priestley and Taylor is as follows, a constant (a) times Penman's radiation term.
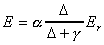
Equating this expression to the combination equation
reveals that the advection term must be a constant fraction of
the radiation term if a
is a constant.

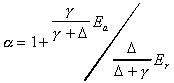
Using micro-meteorological observations over ocean
surfaces and over saturated land-surfaces following rainfall,
Priestley and Taylor came up with a best-estimate of 1.26 for
the parameter a.
The fact that a
is greater than one indicates that true advection-free conditions
do not exist. Since 1972, several other researchers have confirmed
that a values
in the range 1.26-1.28 are consistent with observations under
similar conditions. Some researchers have found significantly
lower values for the a
coefficient, but these coefficients were found for different types
of surfaces (i.e. tall vegetation or bare soil as opposed to grass
and open water). There have also been indications that the a
coefficient may exhibit significant seasonal
variation (Brutsaert, p. 221).
Priestley-Taylor estimates have shown good agreement
with lysimeter measurements for both peak and seasonal evapotranspiration
in humid climates; however, the Priestley-Taylor equation substantially
underestimates both peak and seasonal evapotranspiration in arid
climates. The advection of dry air to irrigated crops is likely
to be greater in arid climates because large saturated areas are
rare, resulting in a more dominant role of the advection term.
A higher a
coefficient may be required in arid climates (ASCE, 1990). Based
on arid sites studied in ASCE, 1990, a value of a=1.7-1.75
seems more appropriate for arid regions. Shuttleworth, 1993,
states that the Priestley-Taylor method is the "preferred
radiation-based method for estimating reference crop evapotranspiration."
Shuttleworth, 1993, notes that errors using the Priestley-Taylor
method are on the order of 15% or 0.75 mm/day, whichever is greater,
and that estimates should only be made for periods of ten days
or longer.
4.2.3.3 Comparison of
Pan and Priestley-Taylor Methods
Figure 4.4, Figure 4.5, and Figure 4.6 are maps of
mean annual temperature, mean annual net radiation distribution, and mean annual potential
evapotranspiration made using the Priestley-Taylor method. A
comparison between Figure 4.4 which shows the mean annual Priestley-Taylor
potential evapotranspiration and Figure 4.3 which shows the gross
reservoir evaporation is quite revealing. It is clear that the
highest values of reservoir evaporation are in West Texas with
a decreasing trend moving eastward. The converse is true for
the Priestley-Taylor estimates where the lowest values occur in
West Texas with an increasing trend towards East Texas. The reason
for the non-intuitive, low potential evapotranspiration estimates
from the Priestley-Taylor method in West Texas is that radiation
and temperature data that were measured under non-potential conditions
have been used. The Priestley-Taylor estimates are proportional
to the net radiation (Figure 4.5) at the earth's surface. In
wetter areas of East Texas, there is more water on the land surface
and in the atmosphere to absorb incoming solar radiation and this
results in higher net radiation values. In addition, greater
cloud cover and water vapor in the atmosphere trap a larger percentage
of the longwave radiation emitted from the earth. Spatial variation
of surface albedo (fraction of incident shortwave radiation reflected)
also contributes to this trend because drier, less vegetated areas
in West Texas tend to have higher albedos. In addition to spatial
trends caused by moisture variation, net radiation values increase
from north to south because of the earth's shape and its tilt
relative to the sun. The spatial patterns in Priestley-Taylor
potential evaporation shown in Figure 4.6 reflect the spatial
patterns of temperature and net radiation in Figures 4.4 and 4.5.
Because the net radiation at the earth's surface is directly related to the wetness of the area, it may be a better surrogate for actual evapotranspiration than potential evapotranspiration. In Section 5.23 a map of Bowen ratios for Texas is computed. As discussed in Section 5.3.3, use of net radiation and temperature data, along with a map of Bowen ratios may be an alternative approach to estimating evaporation that eliminates the use of the difficult potential evapotranspiration concept.
Figure 4-4: Mean Annual Temperature in Texas from Legates and Willmott Climatology
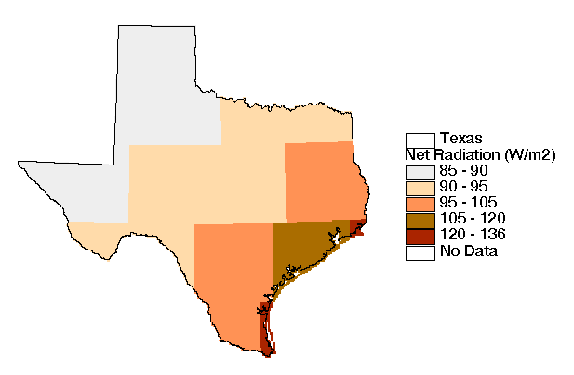
Figure 4-5: Mean Annual Net Radiation Estimates from the ERBE Program
In terms
of absolute magnitude, the statewide average reservoir evaporation
is much higher 1690 mm year-1 than the Priestley-Taylor
estimate 1120 mm year-1; however, the values in East
Texas are more comparable because the lowest reservoir evaporation
estimates and highest Priestley-Taylor estimates both occur here.
Looking at the results of the next section, differences in the
spatial and temporal distribution between the two potential evaporation
estimates make a big difference in the resulting surplus.
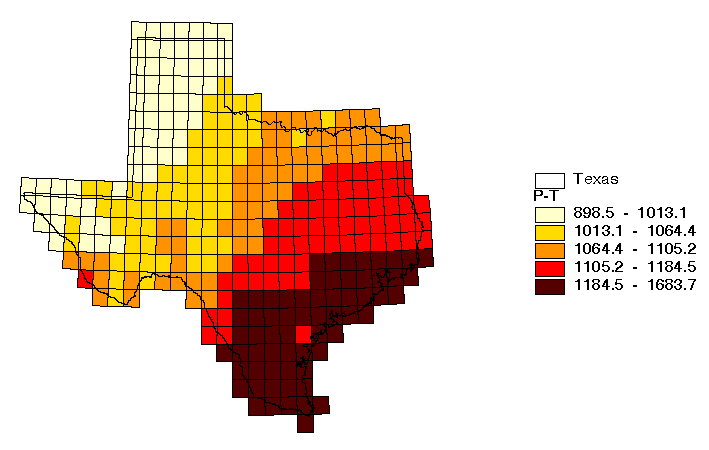
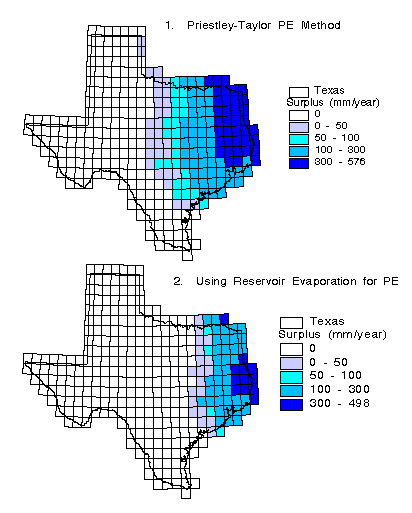
The results from the soil water balance are monthly estimates of evaporation, surplus, and soil moisture in each 0.5 grid cell covering the State. Figure 4.7 shows the mean annual surplus estimated from two separate calculations, the first using the Priestley-Taylor potential evapotranspiration method and the second using the reservoir evaporation as potential evapotranspiration. Using the Priestley-Taylor potential evapotranspiration method yields an average of 85 mm year-1 of surplus across the State while the use of the reservoir evaporation method yields 42 mm year-1 and the observed runoff (78.4 mm year-1 from Section 5) is somewhere between these two estimates. A major problem is that this soil-water balance model predicts zero runoff for much of the State even though it is known that some runoff occurs in these areas. The time distribution of precipitation, actual evaporation, soil moisture, and surplus for two cells are shown in Figure 4.8. In the cell on the left, the water-holding capacity (162.5 mm) is never reached, but for the cell on the right the water-holding capacity (91 mm) is exceeded during seven months out of the year and surplus is generated.
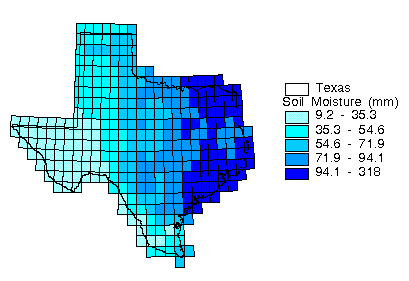
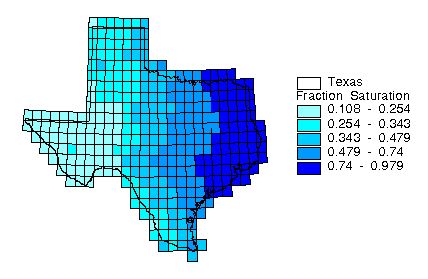
The effects of that the water-holding capacity estimate
has on soil-water budget can be seen in Figures 4.9 and 4.10.
Figure 4.9 shows the mean annual soil moisture [mm] and Figure
4.10 shows the mean annual soil moisture divided by the water
holding capacity. The differences in Figure 4.9 and 4.10 occur
where the soil water-holding capacity has a limiting effect on
evaporation relative to surrounding cells.
The rudimentary soil-water balance approach used
in this study provides a qualitative sense of how precipitation
is partitioned between runoff, evaporation, and soil moisture
storage. The surplus and soil moisture values computed with this
model are interpreted better as indexes of relative wetness rather
than absolute estimates because none are calibrated against measured
values. Use of a monthly time step, a simplified representation
of soil and plant hydrology, the ambiguity in applying the potential
evapotranspiration concept to dry areas, and the errors in estimating
potential evapotranspiration are major limitations of this model.
The model time step cannot account for storm runoff, an important
mechanism for runoff generation. The soil-water balance model
is an incomplete hydrology model because it is very difficult
to calibrate against observed values. Coupling a soil-water balance
model with measured runoff is the only realistic way to derive
accurate runoff estimates. A simplified coupling of the soil-water
balance model to a surface runoff model was achieved in a recent
study to develop a GIS-based water planning tool for the Niger
River Basin in West Africa (Maidment et al., 1996; http:
// www.ce.utexas.edu / prof / maidment / GISHydro / africa / africa.htm).
This model was calibrated for monthly flows but not validated.
A more detailed approach to this type of study could be taken
by implementing a continuous stream flow simulation model with
daily time stepping (or less); however, implementing this type
of model on a region the size of Texas is a formidable task.