2.0 LITERATURE
REVIEW
2.1 Atmospheric Water Balance Studies
A number of researchers have used the atmospheric
water balance to estimate hydrologic fluxes. Among these researchers,
Rasmusson, 1967, Brubaker et al., 1994, and Oki et al.,
1995, describe atmospheric water balance studies at river basin,
continental, and global scales. Rasmusson, 1967, analyzes the
characteristics of total water vapor flux fields over North America
and the Central American Sea. A noteworthy observation made by
Rasmusson is that a large diurnal wind system covering the central
United States, part of Mexico, and the Central American Sea produces
significant diurnal variations in the transport of water vapor.
By decomposing the vertically integrated vapor flux term into
mean motion and transient eddy terms, where the mean motion term
is at a time scale of one month and the transient eddy term describes
motion at a time scale of less than one month, Brubaker et.
al. also observe important vapor flux transport at sub-monthly
time scales. Brubaker et. al. note that poleward eddy
flux transport from the Gulf of Mexico is significant, particularly
during the winter months. From these observations, Brubaker et.
al. surmise that the use of monthly-averaged or sparse data
may significantly underestimate the eddy flux component of vapor
transport. These observations are relevant to the interpretation
of our results, as discussed in Section 3.3. Brubaker et al.
also note that the accuracy of runoff estimates made using atmospheric
data increases with the size of the study area and cite a recommendation
by Rasmusson, 1977, that a minimum area of 106 km2
should be used . The area of Texas is about 0.7 x 106
km2. Improvements in observational networks and general
circulation models may justify runoff estimation on smaller areas
in the future.
If the annual change in atmospheric water storage
and surface water storage are both negligible, runoff estimates
can be obtained from the vertically integrated vapor flux convergence
(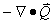 ).
Using four years of data from the European
Centre for Medium-Range Weather Forecasts (1985-1988), Oki et
al. compared convergence
values with the observed annual runoff for
70 river basins throughout the world. Differences between vapor
flux convergence and measured runoff varied widely, although larger
river basins tended to show smaller differences. On average,
the vapor flux convergence was about 2/3 of the measured runoff.
Oki et al. also made a more detailed study of the Chao
Phraya River basin in Thailand which drains 178,000 km2.
Oki et al. estimated annual runoff, monthly evaporation,
and monthly storage for the Chao Phraya from 1985 to 1988. The
evaporation and river basin storage values were estimated by augmenting
atmospheric data with precipitation and runoff data. In the Chao
Phraya basin, the vapor flux convergence was consistently higher
than observed runoff; however, the temporal variations of vapor
flux convergence and runoff were comparable. This was illustrated
by applying a reduction factor to the convergence
values.
).
Using four years of data from the European
Centre for Medium-Range Weather Forecasts (1985-1988), Oki et
al. compared convergence
values with the observed annual runoff for
70 river basins throughout the world. Differences between vapor
flux convergence and measured runoff varied widely, although larger
river basins tended to show smaller differences. On average,
the vapor flux convergence was about 2/3 of the measured runoff.
Oki et al. also made a more detailed study of the Chao
Phraya River basin in Thailand which drains 178,000 km2.
Oki et al. estimated annual runoff, monthly evaporation,
and monthly storage for the Chao Phraya from 1985 to 1988. The
evaporation and river basin storage values were estimated by augmenting
atmospheric data with precipitation and runoff data. In the Chao
Phraya basin, the vapor flux convergence was consistently higher
than observed runoff; however, the temporal variations of vapor
flux convergence and runoff were comparable. This was illustrated
by applying a reduction factor to the convergence
values.
Significant uncertainties in runoff estimation using
atmospheric data still exist even at the continental scale. Both
Brubaker et al. and Oki et. al. compare their continental
runoff estimates with those given by Baumgartner and Reichel,
1975, for river runoff. For North America, Brubaker et. al.
estimate annual runoff as 84.6 mm/year while Oki et. al.
estimate 263 mm/year and Baumgartner and Reichel give 223 mm/year.
Both Brubaker et al. and Oki et al. make note of
the fact that poorly defined continental or basin boundaries may
contribute to inaccuracies in runoff estimation. This problem
is solved in the current study of Texas by using a geographic
information system in which any arbitrarily defined boundary can
be used to compute the water balance, although the problem remains
that atmospheric soundings are sparse.
2.2 Soil Water Balance Studies
Where detailed data about soil layers, depth to groundwater,
and vegetation are not available, hydrologists have often resorted
to simple bucket models and budgeting schemes to model near-surface
hydrology. Despite numerous uncertainties associated with the
simple soil-water budget model like the one used in this study,
many researchers have applied this type of model to problems ranging
from catchment scale studies to the global water balance and climate
change scenarios (Thornthwaite, 1948; Shiklomanov, 1983; Manabe,
1969; Mather, 1978; Alley, 1984; Willmott et al., 1985;
Mintz and Walker, 1993; Mintz and Serafini, 1992). This approach
is attractive because of its simplicity. The simple "bucket"
model used here requires minimal input data: precipitation, potential
evapotranspiration, and soil-water holding capacity. The studies
by Willmott et al., Mintz and Walker, and Mintz and Serafini,
are climatological studies that present the global distributions
of precipitation, evapotranspiration, and soil moisture. Mintz
and Serafini compare their evapotranspiration estimates for sixteen
major river basins throughout the world with those derived from
river runoff analysis made by Baumgartner and Reichel, 1975, and
the values show reasonable agreement.
At a smaller scale, Mather, 1978, (Chapter 4) describes
the application of a soil-water budget model to several watersheds
in the coastal plains of Delaware, Maryland, and Virginia. Comparisons
between measured and computed runoff values are rather poor for
monthly data, but better for annual data, although Mather suggests
further refinement of the method even for annual values. In its
simplest form, the soil-water budget model does not account for
situations where the precipitation rate is greater than the infiltration
capacity of the soil. Mather describes one approach to remedy
this problem, that is, to first use the SCS method to estimate
direct overland runoff and subtract this amount from the precipitation
before it is allowed to enter the soil "bucket." This
approach appears to yield better results (Mather, Chapter 4).
A similar approach of taking an initial rainfall abstraction
before allowing precipitation to enter the soil column for climatological
budgeting was used in a study of the Niger Basin described by
Maidment et al., 1996 (further description available at
http://www.ce.utexas.edu/prof/maidment/gishydro/africa/africa.htm).
In the Niger Basin study, the surplus from the soil-water budget
is passed to a surface and groundwater routing model which is
in turn calibrated with observed runoff.
2.3 Surface Water Balance Studies
2.3.1 Water Balances of Texas
The surface water balance, a commonly used method
in hydrologic studies, relies on the fact that with the exception
of coastal areas, the landscape can often be divided into watershed
units from which there is only one surface water outflow point.
Provided that the average watershed precipitation and runoff
can be measured with reasonable accuracy, the annual evaporative
losses from a watershed can be estimated. Of course this assumes
that change in storage is negligible and that there are no significant
inter-watershed transfers via groundwater or man-made conveyance
structures. Empirical relationships are often used to estimate
mean annual or mean monthly flows in ungaged areas; this approach
is used in this study.
Two water balance studies that are particularly relevant
to Texas are those by Ward, 1993, and the Texas Board of Water
Engineers, 1961. Ward presents a water balance similar to that
described here in which he estimates precipitation, evapotranspiration,
runoff, recharge, and water demands for four different hydroclimatological
regions in Texas and for the State as a whole. To estimate annual
runoff, Ward uses an empirical relationship between rainfall and
runoff. A similar approach is used in this study, although the
rainfall-runoff relationship derived here is used in conjunction
with a large database of measured values to develop spatially
distributed maps of runoff. The Texas Board of Water Engineers
(TBWE; now Texas Water Development Board) Bulletin 6001 is a study
of surface runoff (1940-1956) from the major basins and sub-basins
in Texas that uses measured flow data. To estimate runoff in
ungaged watersheds or watersheds with insufficient streamflow
records, the authors of Bulletin 6001 used a proportion of the
observed runoff in a watershed with similar characteristics and
an additional factor to account for the difference in precipitation
if necessary. One product of Bulletin 6001 is a map of Texas
sub-basins with printed values of runoff. Improvements in computer
technology since 1961 allow for more detailed electronic maps
to be generated in this study, although the idea of mapping runoff
values is similar.
2.3.2 Runoff Mapping
Three recently published articles by Arnell, 1995;
Lullwitz and Helbig, 1995; and Church et al., 1995, describe
studies of runoff mapping. All three use a geographic information
system (GIS) to manage spatial data at a regional or continental
scale. The paper by Arnell summarizes five approaches for deriving
gridded runoff maps at a 0.5 grid resolution including (1) simply
averaging the runoff from all stations within each grid cell,
(2) statistically interpolating runoff between gages, (3) using
an empirical relationship that relates runoff to precipitation,
potential evaporation, and temperature, (4) using a soil-water
balance type model, and (5) overlaying grid cells onto catchment
runoff maps to derive area-weighted runoff estimates. Arnell
evaluates all but method (4) by mapping runoff onto 0.5 grid cells
over a large portion of western Europe, and then intersecting
the results with seven gaged river basins to validate the results.
The results show that method (5) produces the most reasonable
estimates. In a study similar to that of Arnell, Lullwitz and
Helbig created 0.5 runoff maps for the Weser River in Germany.
Both Arnell and Lullwitz and Helbig note that 0.5 runoff maps
can be useful for validating general circulation models (GCM's).
Church et. al. present maps of evapotranspiration (ET)
and runoff/precipitation (R/P) ratios for the northeastern United
States. Church et. al. use an interpolation method to
create runoff maps. Church et al. found their results
to be useful in assessing the effects of acidic deposition.
The approach used for runoff mapping in this study
is different than any of the methods described above, although
it is most similar to Arnell's method 5. The approach taken here
combines an empirical rainfall-runoff relationship and watershed
runoff balancing.
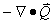 ).
Using four years of data from the European
Centre for Medium-Range Weather Forecasts (1985-1988), Oki et
al. compared convergence
values with the observed annual runoff for
70 river basins throughout the world. Differences between vapor
flux convergence and measured runoff varied widely, although larger
river basins tended to show smaller differences. On average,
the vapor flux convergence was about 2/3 of the measured runoff.
Oki et al. also made a more detailed study of the Chao
Phraya River basin in Thailand which drains 178,000 km2.
Oki et al. estimated annual runoff, monthly evaporation,
and monthly storage for the Chao Phraya from 1985 to 1988. The
evaporation and river basin storage values were estimated by augmenting
atmospheric data with precipitation and runoff data. In the Chao
Phraya basin, the vapor flux convergence was consistently higher
than observed runoff; however, the temporal variations of vapor
flux convergence and runoff were comparable. This was illustrated
by applying a reduction factor to the convergence
values.
).
Using four years of data from the European
Centre for Medium-Range Weather Forecasts (1985-1988), Oki et
al. compared convergence
values with the observed annual runoff for
70 river basins throughout the world. Differences between vapor
flux convergence and measured runoff varied widely, although larger
river basins tended to show smaller differences. On average,
the vapor flux convergence was about 2/3 of the measured runoff.
Oki et al. also made a more detailed study of the Chao
Phraya River basin in Thailand which drains 178,000 km2.
Oki et al. estimated annual runoff, monthly evaporation,
and monthly storage for the Chao Phraya from 1985 to 1988. The
evaporation and river basin storage values were estimated by augmenting
atmospheric data with precipitation and runoff data. In the Chao
Phraya basin, the vapor flux convergence was consistently higher
than observed runoff; however, the temporal variations of vapor
flux convergence and runoff were comparable. This was illustrated
by applying a reduction factor to the convergence
values.