2.1) HYDROSTATIC FORCES ON A PLANE SURFACE
2.1.1) OBJECTIVES
2.1.2) BACKGROUNDThe hydrostatic force on any surface is due to the fluid pressure acting on that surface, as shown in Fig. 2.1. Pressure is a normal stress which is positive when in compression. Since the pressure is everywhere normal to the surface, the resultant pressure force (Fp) is also normal to the surface. The magnitude of Fp is
| (2.1) |
where p = gysin a,
g = specific weight of the fluid, y = distance
measured from level of zero pressure and measured in the plane of the surface,
and a = angle which the plane of the surface
makes with the horizontal. For constant g and
a,
| (2.2) |
where
= y coordinate of the centroid of the surface and
is the pressure at the centroid of the surface. Fp acts at ycp,
called the center of pressure. The resultant pressure force acting at this
center of pressure must give the same moment as the distributed pressures,
so ycp can be found from
 |
(2.3) |
where Io = moment of inertia about the level of zero pressure
for the surface on which the pressure force is acting and
= moment of inertia about the horizontal centroid axis. Notice that Fp
is calculated using the pressure at the centroid of the surface but the
resultant pressure force acts at ycp which is lower than the
centroid.

Fig. 2.1 - Hydrostatic pressures and pressure force on a plane surface
2.1.3) LABORATORY APPARATUSA photograph of the laboratory apparatus is shown in Fig. 2.2. The basic components are a Plexiglas box for holding water or other liquid, a curved element which has a vertical, plane end, a support bean, and a point gage for measuring the location of the water surface. A schematic diagram is shown in Fig. 2.3.

Fig. 2.2 - Photograph of laboratory apparatus
An essential feature of the apparatus is that the center of curvature for each curved surface is at the point of support on the knife edge. Since pressure is a normal stress, the pressures on the curved surfaces do not cause a moment about the support point. The pressures on the two opposite plane sides of the curved object cancel. As a result, only the forces on the plane surface at the end of the curved surfaces and the weight cause moments about the knife edge.
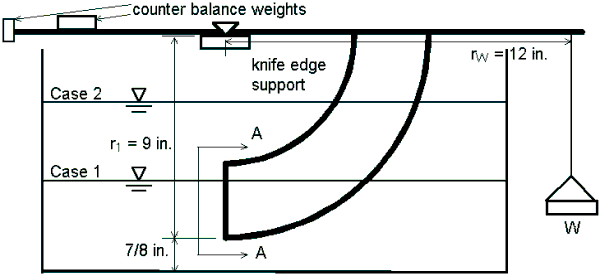
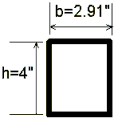
Cross Section A-A
Fig. 2.3 - Schematic diagram of laboratory apparatus
2.1.4) PROCEDURESa) Use the leveling screws on the legs and the level bubble on the top of the support arm to level the tank front to back.
b) Use the weights on the support arm to counter balance the weight of the arm, weighing pan, and Plexiglas curved object in the tank.
Case 1:
c) Place a weight (e.g. 100 g, which is 0.22 lb) in the weighing pan.
d) Fill the tank with water until the support arm is balanced and horizontal. When the support arm is balanced, the moment of the hydrostatic force on the plane end of the curved object equals the moment of the weight in the weighing pan.
e) Use the point gage to determine the depth of water by taking a reading on the bottom of the tank and at the water surface. The difference of these two readings is the water depth.
f) Use the measured depth, the dimensions in Fig. 2.3, Eq. 2.2, and Eq. 2.3 with a = 90o to calculate the pressure force on the plane surface and the moment of that force about the support point.
g) Compare the moment from (f) with the moment of the weight in the weighing pan.

Fig. 2.4 - Case 1
Case 2:
h) Repeat (c) - (g) for another weight (e.g., 250 g, which is 0.55
lb).
CASE 2
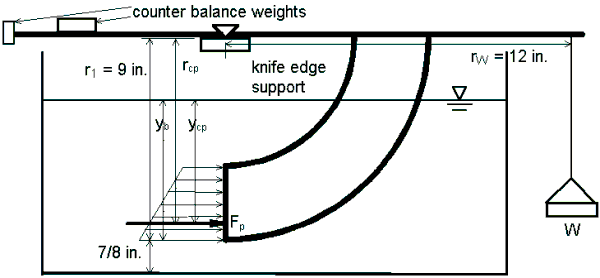
Fig. 2.5 - Case 2
2.2) ARCHIMEDES' PRINCIPLE OF BUOYANT FORCES
2.2.1) OBJECTIVES
2.1.2) BACKGROUNDA buoyant force is the resultant pressure force acting on an object. The reason that this force is equal to the weight of the displaced fluid can be seen by considering pressure forces acting on an increment of the surface area of the object and then integrating the pressures over the area to obtain the resultant force. First, consider the vertical strip through the submerged object in Fig. 2.6. The pressure force on the bottom is (dFp)1 = p1dA1. The vertical component of this force is (dFpv)1 = p1dA1cos(q1), but dA1cos(q1) = dAh, which is the horizontal projection of dA2. Thus, (dFpv)1 = p1dAh. In the same way, the vertical component of the pressure force on the top is (dFpv)2 = -p2dAh. The minus sign comes from the fact that the force is acting in the negative z direction. The net vertical force on the vertical strip is then
| dFpv = (p1 - p2)dAh |
(2.4)
|
Since pressure is constant in horizontal planes for hydrostatic conditions,
the relationship between p1 and p2 can be found by
considering the pressure variation along the line of length l
away from the object. Then using dp = -gdz,
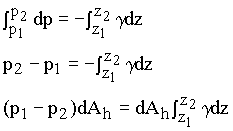 |
(2.5)
|
The right-hand side of the last line of Eq. 2.5 is the weight of water in an incremental volume with a horizontal area of dAh and a length of l (i.e., z2 - z1), that is, it is the weight of water that was displaced by the part of the object in the vertical strip. By integrating these vertical strips throughout the volume of the object, the total vertical force will be obtained and it will be equal to the total weight of the displaced fluid.
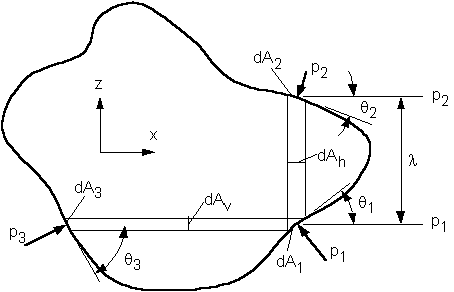
Fig. 2.6 - Pressure forces on a submerged object
There is also a horizontal component of force on each dA. On dA1, the horizontal component is (dFph)1 = -p1dA1sin(q1). On the left-hand side of the object on dA3, (dFph)3 = p3dA3sin(q3). Since dAsin(q) is the vertical projection of the areas, dA1sin(q1) = dAv = dA3sin(q3). Therefore, (dFph)1 = -(dFph)3, so these two forces cancel. The same thing is true all around the object. Thus, there is no net horizontal force.
As a result, the total force comes from the vertical components of the pressure forces, and the buoyant force is equal to the weight of the displaced fluid. Note that it has not been assumed that the specific weight is constant. This derivation proves Archimedesí Principle (only 22 and a half centuries after he figured it out!).
Recall that a vector, in this case the buoyancy force, has magnitude, direction, and location. The derivation above gives the magnitude. The direction is vertically upward. Since the net force comes from only the vertical components of the incremental pressure forces, the resultant must be vertical. Furthermore, it is upward since the pressures on the bottom of the object are larger than the ones on the top. The resultant force acts through the center of gravity of the displaced water. This result can be proven by taking the moments of the incremental pressure forces discussed above, but the details will not be given here.
This derivation has been for a submerged object. Archimedesí Principle applies to floating objects also. The proof is essentially the same as for a submerged object. The primary difference is that the pressure is essentially constant on the part of the object in the air.
2.2.3) LABORATORY APPARATUSThe apparatus is a 1000 cc graduated cylinder and a hydrometer. These items were also used in one of the laboratory experiments on fluid properties.
2.2.4) PROCEDURES
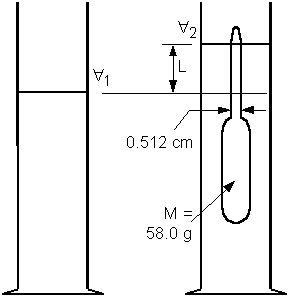
Fig. 2.7 - Graduated Cylinder