THIS INTERACTIVE JAVA APPLET WAS DEVELOPED AT UT AUSTIN BY Aubrey Dugger, UNDER THE SUPERVISION OF PROFESSOR. Spyros A. Kinnas, 1997.
PERMISSION TO LINK TO THIS JAVA APPLET AND TO DOWNLOAD OR TO USE THE RELATED JAVA SOURCE CODE, MUST BE GRANTED BY PROFESSOR Spyros A. Kinnas ( kinnas@mail.utexas.edu ).
 |
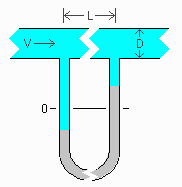
Attached to a cylindrical pipe is a U-tube mercury manometer, as shown. Given the type of fluid in the pipe, the velocity (V), the diameter of the pipe (D), and the length between sides of the U-tube manometer (L), find the change in height (Dh) of the mercury in the manometer. |
The first step in this problem is to determine the type of flow going through the pipe
(i.e. laminar or turbulent). To do this, we need to find the Reynold's number (Re).
This is accomplished fairly painlessly if we know the velocity, pipe diameter, and
fluid viscosity. The equation is:
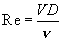
where n = the kinematic viscosity of the fluid.
Once we know the Reynold's number, we can approximate the flow as:
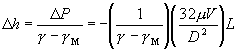
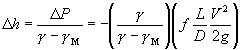
All of the variables in this equation are known except for the friction factor, f.
To find this value, we can either consult the Moody diagram with our known Reynold's
number, or we can solve the equation:
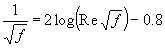
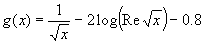

Our first initial guess (xk-1) is 0.01. Our second guess (xk)
is this number plus 1%, or 1.01(xk-1)=0.0101.
We then plug these guesses into the Newton-Raphson equation to find a new guess, xk+1. This becomes our new xk and our previous xk gets promoted to our new xk-1. This entire process is repeated until the function converges, or the difference between our two guesses is minimal. The final value of x is the friction factor (f) we are looking for.
Once we determine the friction factor for the given flow conditions, we can plug all of our variables into the equation and solve for the change in height of the mercury in the manometer tube.
 Go to Viscous Drag Applet
Go to Viscous Drag Applet